Chapter : 3 MEASURES OF CENTRAL TENDENCY

Chapter : 3    MEASURES OF CENTRAL TENDENCY

The frequency distribution summarizes the given mass of data, but for practical purposes there is usually a need for further condensation, particularly when we want to compare two or more different distributions.  We may even reduce the entire distribution to one number which represents the distribution.  We calculate ‘Measures of central tendency’ for this purpose.  These measures summarize the given mass of data in much more concise fashion than a frequency distribution.  Frequency distribution has too many details while an average reduces the large number of observations to one figure.

The term ‘averages’ is used very often e.g., average Indian, average marks, or average size, etc.,  Sometimes it means ‘typical or usual’ like average Indian.  It may also refer to the result of a specific process of calculation like average marks of students.

Average is used to reduce two or more aggregates to a common denominator, in order to make comparisons.  It can be used to compare the totals for time periods of different lengths, e.g., if we have the figures of production for time periods of different lengths, e.g., if we have the figures of production for the months of January and February, in 1985 the production for the month of January is 4000 units while for the month of February it is 3640 units.  We cannot compare the two figures, 4000 and 3640 units.  The reason is, January has 31 days while February has 28 days.  Here we find the average daily production by dividing the total by the number of days.  The average daily production of January is 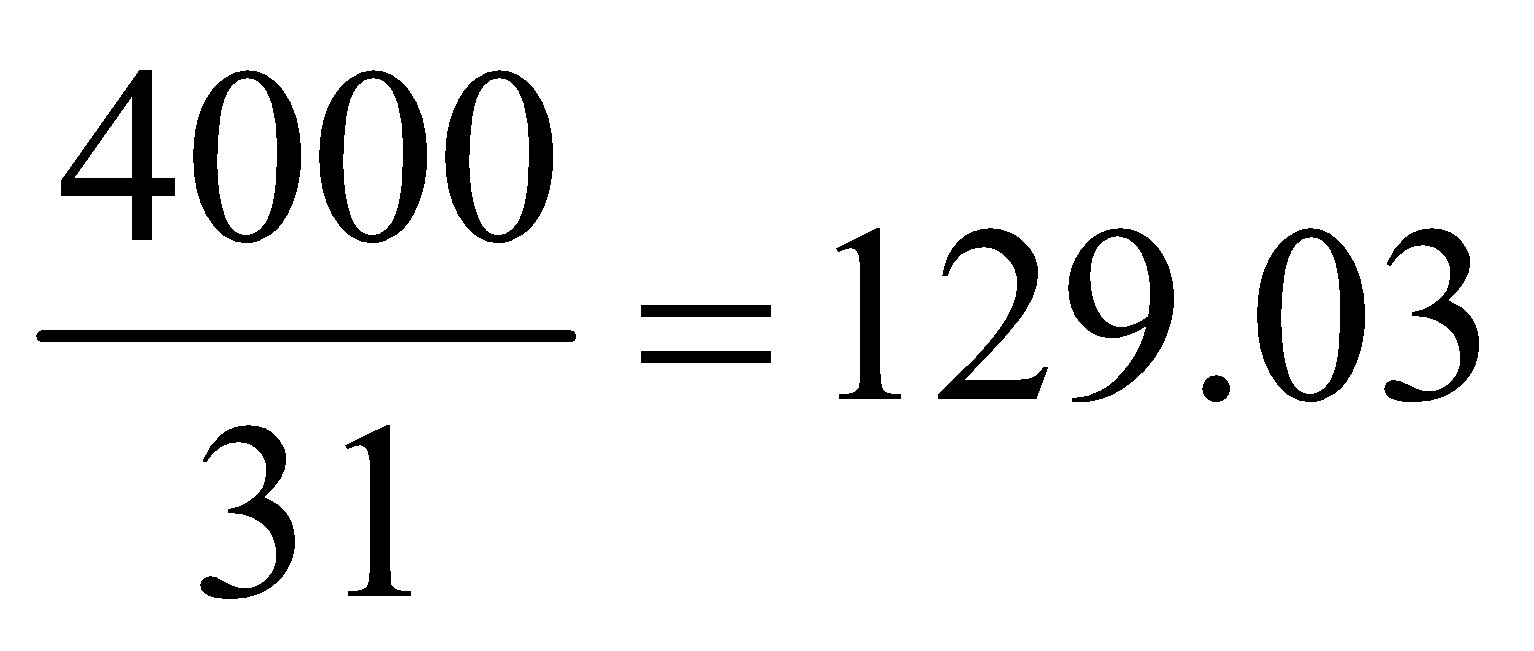units while the average daily production of February is 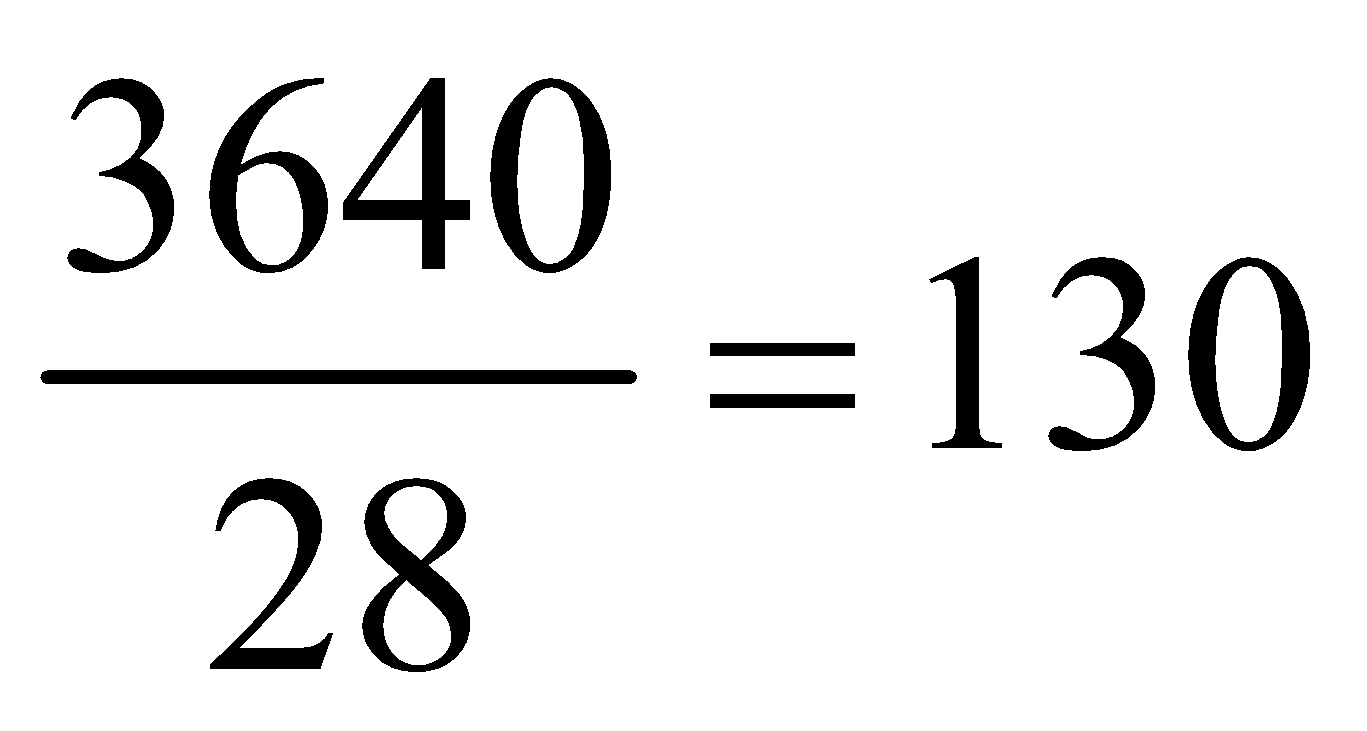units i.e., There is no significant difference between the production rate for the two months.  Though the total production in February is less, the daily production rate is almost the same.

The number of deaths due to traffic accidents in two different periods should not be compared directly.  The number should be compared with the total population and deaths per thousand should be calculated.  The number of accidents is affected by the number of vehicles on the road and therefore we can also compare the number of accidents per 100 vehicles.

Averages are also used as a measure of typical size.  It gives one figure that is typical of all the observations that are essentially different.  If the items are scattered, the measure will not be very satisfactory while for homogeneous data the average will be a good representative of the data.  But it is necessary to have this kind of summary statement for many statistical data.

There are five averages which are conceptually different and each of them is from some point of view of a ‘central’ value of the distribution.  The averages are also referred to as ‘measures of central tendency’ because they are used to describe a magnitude near the centre of a distribution about which the values cluster.

If we have the distribution of marks of students, very few students will get marks like 4, 5, 8, …. and similarly there will be a small number of students getting above 80.  Most of the students will have marks between 40 and 60 and the average will be somewhere within these limits, that is, average is a central figure.  Averages are also known as ‘measures of location’.

Each of these averages has its own advantages and disadvantages.  But there are certain characteristics, which make the average a good representative of the given data.  

DESIDERATA FOR SATISFACTORY AVERAGE

1. An average should be rigidly defined; otherwise its value will be affected by the bias of the person who calculates it.  It cannot be a good representative if it is not a fixed value.
2. It should be based on all the observations.  It sill not be a good representative if some observations are left out of calculation.
3. It should be easy to calculate and easy to understand.  If the calculations requires tedious mathematical process, it will not be understood by many and it use will be limited.
4. It should be capable of further algebraic treatment.  This makes the average more useful.
5. It should not be affected much by sampling fluctuations.  If two independent samples are taken from the same population, the average should not differ significantly.

It should also be remembered that the average should be expressed in the same unit as the series given.  i.e., If we have the heights of 50 children in cms and the average is 130, it should be written as 130 cms.  If the income of 100 families are given in (’00 Rs.) and the average is 30, the average should be expressed as 30(100 Rs.) or Rs.3000/-.  Now we consider the types of averages.  

ARITHMETIC MEAN:

Arithmetic mean is defined as the sum of all the observations in the distribution divided by the number of observations, i.e.,  if a variable x takes the values 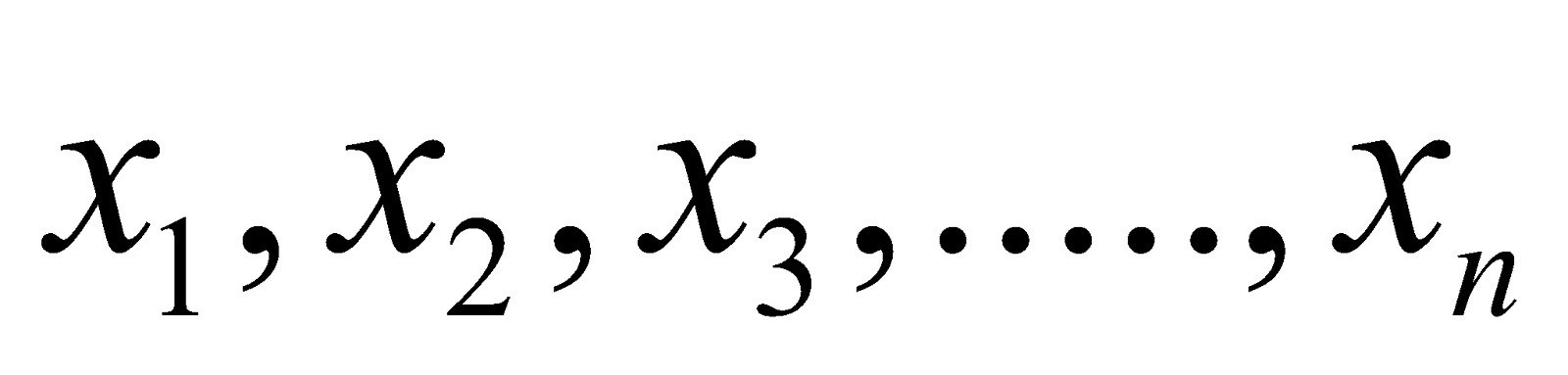, its arithmetic mean is defined as

                                          

                                             i.e.,             

If a variable x tames values 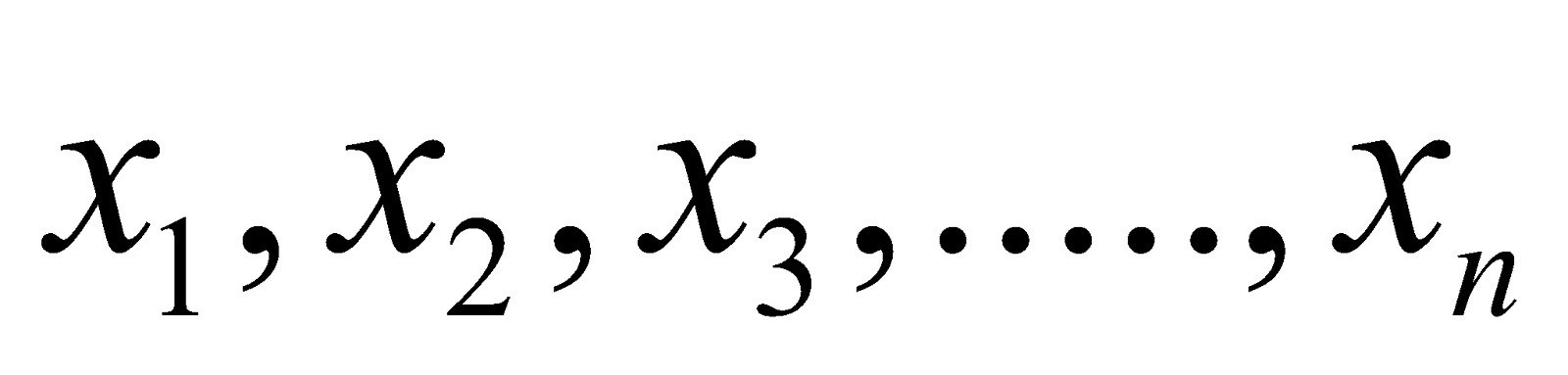with corresponding frequencies , then their arithmetic mean is defined as

                                  

Short-cut Method:

                                                        

Where A is the assumed mean chosen from xi values,    and c is the length of the class-interval.

Exercise:

1. Find the arithmetic mean for the following sets of observations:
1. 125, 132, 127, 139, 140, 142, 137, 122, 120 and 130
2. 13.1, 15.2, 11.9, 10.2, 12.5, 14.3, 11.2, 10.8
3. 1357, 1454, 1389, 1405, 1485
4. 53, 31, 35, -25, 100, 60, -16, 13, -3, 95

[ Answers: a)  131.4      b) 12.4       c) 1418       d) 34.3 ]

2. Calculate the mean for the following data:

xi:	12	14	16	18	20	22
fi:	5	10	15	12	8	3

[ Answer: 16.6415 ]

3. Calculate the mean for the following distribution:

Size of Shoe:	6	7	8	9	10	11
No. of pairs:	32	40	52	40	32	25

[ Answer: 8.3394 ~ 8 ]

4. Calculate the mean for the following data:

xi:	5	6	7	8	9	10	11
fi:	11	15	20	16	12	9	4

[ Answer: 7.5287 ]

5. The following data represents frequency distribution of weights of children, find its arithmetic mean.

Wt. in Kgs.	11	12	13	14	15	16
No. of Children	7	11	15	13	9	4

[ 13.305 kgs ]

6. The following data represents distribution of marks (out of 10) for a class of students.  Find the arithmetic mean.

Marks:	0	1	2	3	4	5	6	7	8	9	10
No. of Students:	2	4	5	7	11	15	13	10	7	3	1

[ Answer: 5.06 ]

7. Find the arithmetic mean for the following distribution:

Marks:	0-10	10-20	20-30	30-40	40-50
No. of students	6	11	15	8	3

[ Answer: 22.91 ]

8. Calculate the arithmetic mean for the following data giving daily wages of workers.

Wages in Rs.:	20-40	40-60	60-80	80-100	100-120	120-140
No. of workers:	7	12	16	13	13	4

[ Answer: 77.69 ]

9. Find the mean for the following data:

Age in years	No. of persons
Less than 10 Less than 20 Less than 30 Less than 40 Less than 50 Less than 60	15 33 54 80 97 100

[ Answer: 27.1 ]

10. Find the arithmetic mean for the following:

Daily wages:	5-15	15-25	25-35	35-45	44-55	Ans: 31.54
No. of persons:	3	8	13	10	5

11. Calculate the arithmetic mean for the following data representing monthly salary of a group of employees.

Salary in Rs.:	700-800	800-900	900-1100	110-1500	1500-1600
No. of persons:	32	43	55	22	18

[ Answer: Rs.1012.06 ]

12. Find the mean for the following data.

Class Interval:	20-30	30-50	50-70	70-90	90-100
Frequency:	9	14	20	12	5

[ Answer: 57 ]

13. Calculate the arithmetic mean:

Sales in ‘000 Rs.:	5-10	10-15	15-25	25-35	35-45	45-50
No. of shops:	2	8	12	15	11	5

[ Answer: Rs.27.97 ]

14. The following data represents yield per acre (in kgs.) for a number of farms.  Find the arithmetic mean.

Yield per acre:	700-750	750-800	800-850	850-900	900-950	950-1000
No. of farms:	32	43	55	22	17	18

[ Answer: 825.8 kgs. ]

15. The following is the distribution of heights in cms of 50 students.  Find the mean.

Height in cms:	140-145	145-150	150-155	155-160	160-165
No. of students:	7	10	15	13	5

[ Answer: 152.4 cms ]

16. Find the arithmetic mean:

Height in cms:	148-152	152-156	156-160	160-164	164-168	168-172	172-176
No. of persons:	3	5	9	15	10	6	2

[ Answer: 162 cms ]

17. The following data represents the distribution of balance amounts in bank accounts at the end of March 2002.  Find the average balance amount.

Amount in Rs.:	500-599	600-699	700-799	800-899	900-999	1000-1099	1100-1199	1200-1299
No. of accounts:	25	42	55	70	62	50	35	11

[ Answer: Rs.877.21 ]

18. Find the average tax for the following data.

Tax in Rs.:	100-399	400-699	700-999	1000-1299	1300-1599	1600-1899
No. of Employees:	12	20	25	35	15	8

[ Answer: Rs.966.89 ]

19. Find the arithmetic mean for the following data.

No. of units produced:	50-99	100-149	150-199	200-249	250-299	300-349	350-399
No. of factories:	4	9	11	15	12	8	2

[ Answer: 218.76 ]

20. The following data represents salary of employees in an office.  Find the average salary.

Salary in Rs.:	No. of Employees.
900 – 1000 1000 – 1200 1200 – 1400 1400 – 1600 1600 – 1800 1800 – 1900 1900 – 2000	4 11 19 22 18 9 3

[ Answer: Rs.1473.26 ]

21. If the mean for the following data is Rs.56/-, find the missing frequency.

Wages in Rs.:	30-40	40-50	50-60	60-70	70-80	80-90
No. of persons:	10	20	40	…	8	6

[ Answer: 16 ]

22. If the average marks of students are 26.75, find the number of students belonging to the class interval 10 – 20.

Marks:	0 - 10	10-20	20-30	30-40	40-50
No. of students:	3	…	15	10	5

[ Answer: 7 ]

23. If the average wages of workers are Rs.73.25, find the number of workers with wage between Rs.80 and Rs.100.

Wages in Rs.:	20-40	40-60	60-80	80-100	100-120	120-140
No. of persons:	10	18	22	…	11	5

[ Answer: 14 ]

24. If the mean value for the following data is 33, find the missing frequency.

Marks:	0-10	10-20	20-30	30-40	40-50	50-60
No. of students:	5	10	25	30	…	10

[ Answer: 20 ]

25. Find the missing frequencies if the mean is 21.9 and the total of frequencies is 75.

Class Interval:	0-5	5-10	10-15	15-20	20-25	25-30	30-35	35-40
Frequencies:	2	5	7	…	…	16	8	3

[ Answer: 13 and 21 ]

COMBINED ARITHMETIC MEAN

If   and are the number of observations of two groups with means 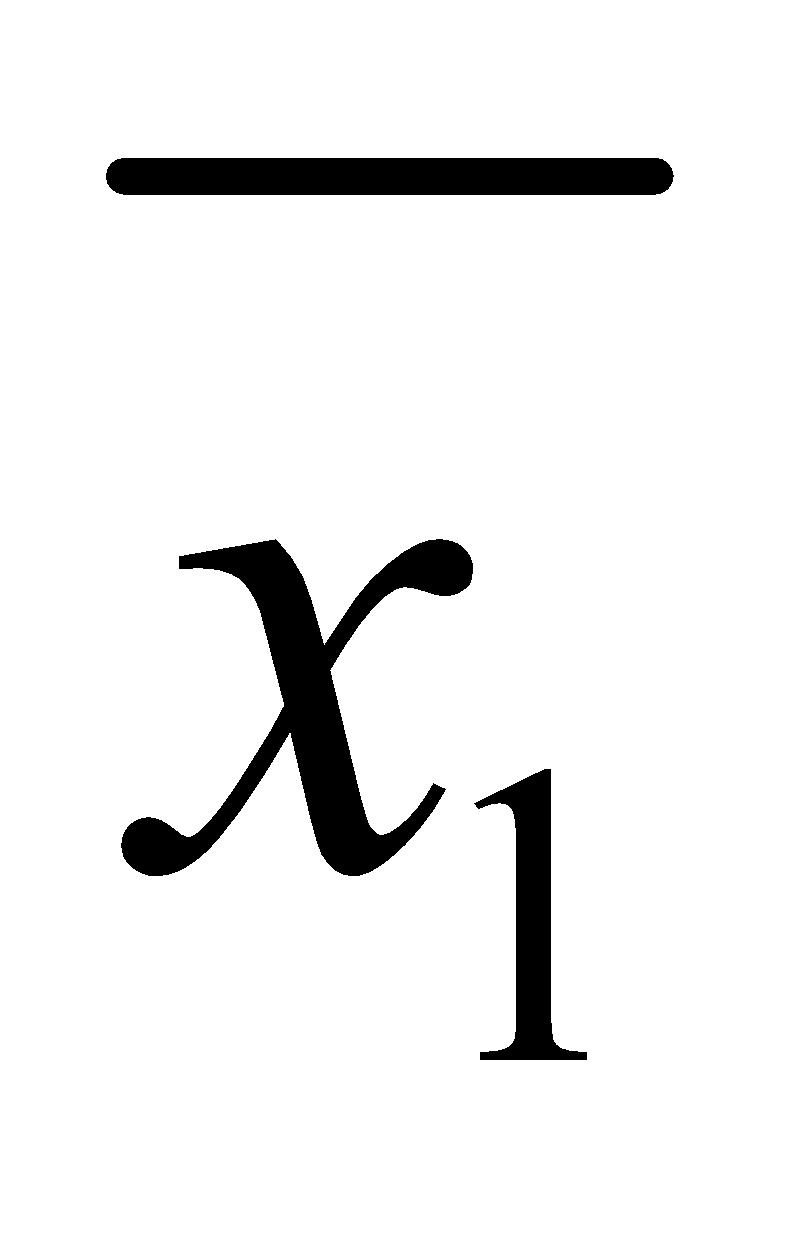and then their combined arithmetic mean, denoted by is given by

This can be extended to three groups also as

PROBLEMS:

1. The average marks of a group of 100 students in Accountancy are 60 and for another group of 50 students, the average marks are 90.  Find the average marks of the combined group of 150 students.   [ 70 marks ]
2. The average daily wages for 90 workers in a factory is Rs.59/-, the average wages for 50 male workers out of them is Rs.63/-.  Find the average wages for the remaining female workers.           [ Rs.54/- ]
3. The average marks of a class of students are 76.  The average marks of boys and girls are 69 and 83 respectively.  If there are 100 boys in the class find the number of girls in the class.   [ No. of girls = 100 ]
4. The mean daily wages of a group of employees are Rs.180/- The mean daily wages of men and women are Rs.186/- and Rs.175/- respectively.  Find the ratio of men and women in the group.     [ 5 : 6 ]
5. If the average marks in a certain test of boys and girls in a class are 80 and 85 respectively and if the average marks for the entire class are 83.75, find the percentage of boys in the class.  [ 25% ]
6. The mean weight of a group of 70 workers is 60 kgs.  The second group consists of 80 workers with average weight 57 kgs and there are 50 workers in the third group with average weight 62 kgs.  Find the average weight of the combined group of 200 workers.   [ 59.3 kgs ]
7. The mean marks of 100 boys in a class are 45.  The mean marks of the entire class of 150 students are 50.  Find the mean marks of the remaining group of girls. [ 60 ]
8. There are three groups in a class of 100 students.  The first contains 25 students with average pocket money Rs.62/-, the second group consists of 50 students with average pocket money Rs.55/-.  Find the average pocket money of the students from the third group if the average for the entire class is Rs.58/-.  [ Rs.60/- ]
9. The average monthly salary of employees of a firm is Rs.5200/-.  The average salaries of gents and ladies from the firm are Rs.6000/- and Rs.4800/- .  Find the percentage of gents and ladies in the firm.   [ 1 : 2 ]
10. A garment factory makes both men’s and women’s shirts.  The average profit of the factory is 8% of sales.  Average profit on men’s shirt is 10%.  Women’s shirts form 60% of the total sales.  What is the average profit on sales of women’s shirts?   [ 6.67% ]
11. There are men, women and children working in a factory.  The total number of workers is 500.  The average daily wages of 250 male workers is Rs.100/-.  The average daily wages of 150 women workers is Rs.80/-.  What is the average daily wages of children working in that factory, given that the average daily wages of all the 500 workers taken together is Rs.82/-   [ Rs.40/- ]
12. The sum of the deviations of a certain number of observations measured from 4 is 72 and the sum of the deviations of the same observations from 7 is -3.  Find the number of observations and their mean.   [ 25  &  6.88 ]
13. The mean of a certain number of observations is 40.  If two more observations with values 50 and 64 are added to the data, the mean rises to 42.  Find the number of items in the original data.      [ 15 ]
14. The mean weight of 98 students as calculated from a frequency distribution is found to be 50 kgs.  It is later discovered that the frequency of the class interval 30 – 40 was wrongly taken as 8 instead of 10.  Calculate the correct arithmetic mean.  [ 49.7 kgs ]
15. The mean monthly salaries paid to all 77 employees in a company was Rs.78/-.  The mean monthly salaries of 32 of them was Rs.75/- and that of the other 25 was Rs.82/-.  What was the mean salary of the remaining?   [ Rs.77.80 ]

MEDIAN

Definition:  

If 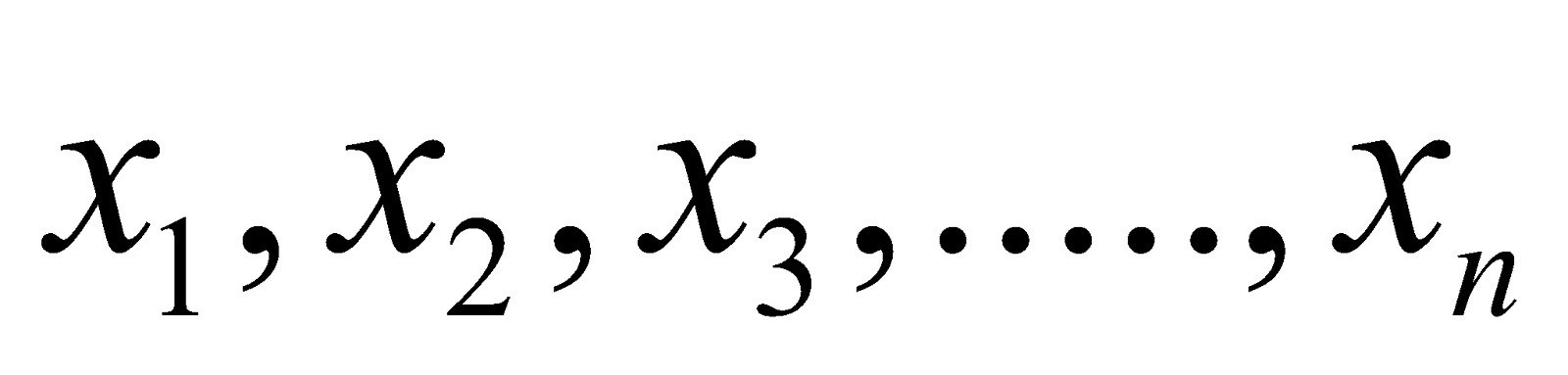are n observations arranged either in ascending order or in descending order and if

1. n is ODD, then there will be only one middle term and the value of the middle term is the median. i.e., Median = .
2. n is EVEN, then there will be two middle terms, the average of the values of the two middle terms is the median. i.e., Median = .

In the case of a frequency distribution, it is calculated as

Median =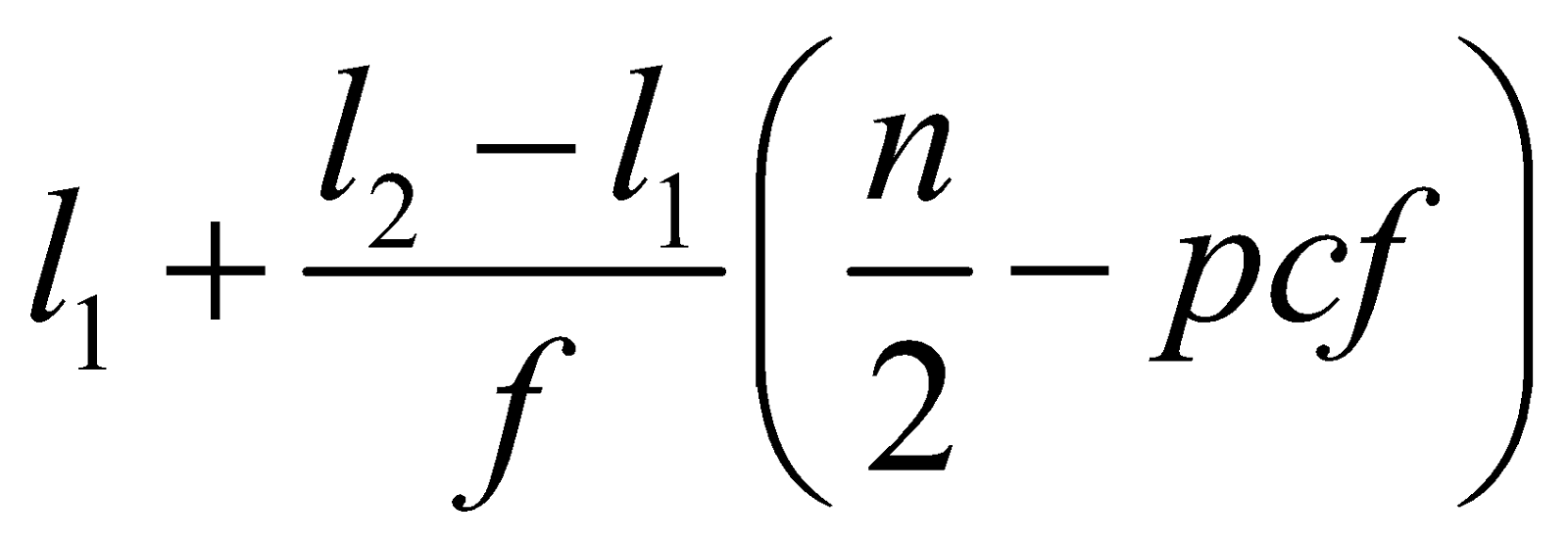

Where 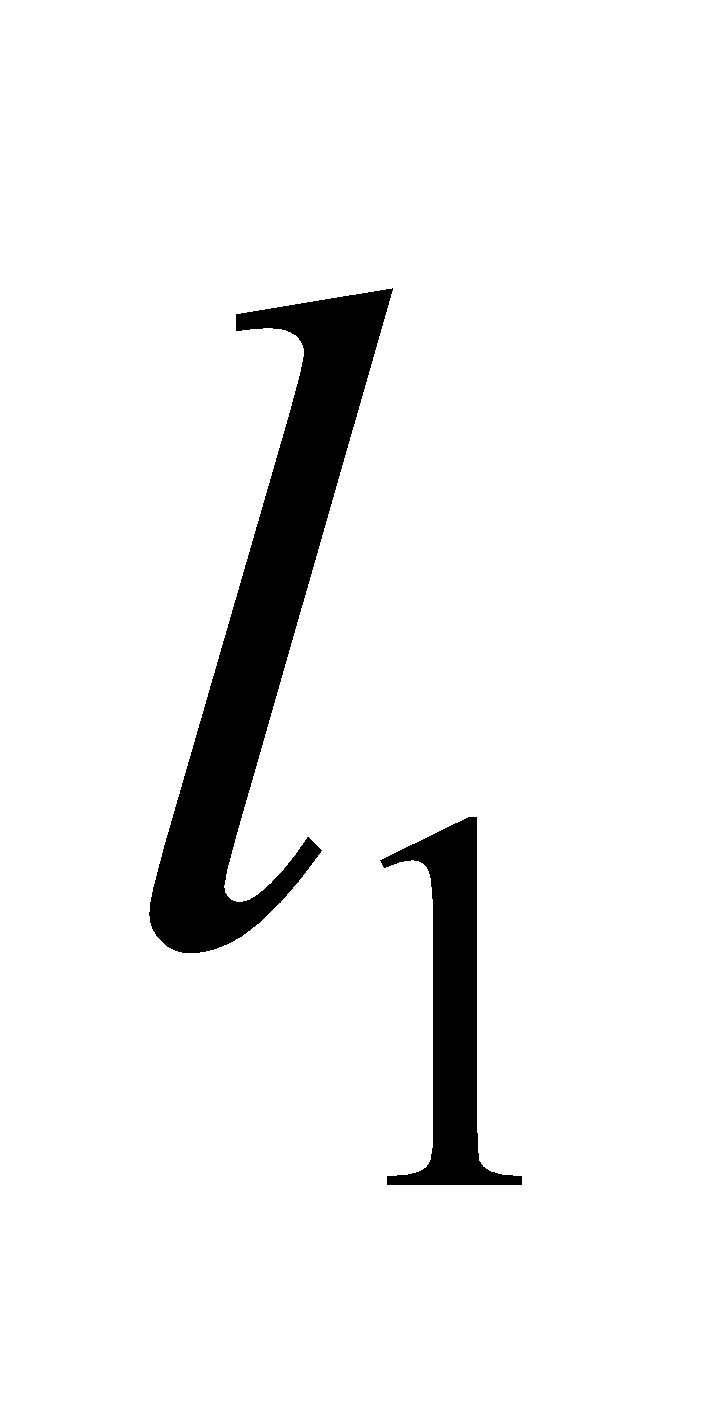is the lower limit of the C.I. of the median class

is the upper limit of the C.I. of the median class

n   is the total of frequencies

is the frequency at the median class

is the previous cumulative frequency

Note:

1. The very first cumulative frequency value for which becomes less than determines the median class.
2. To calculate the median the class intervals must be continuous. If they are not continuous then we have to make them continuous by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit.
3. The value of median thus calculated must be a value in the C.I. of the median class.

PROBLEMS:

1. Find the median of the following sets of observations:

1. 43, 30, 44, 67, 35, 40, 59         [ 43 ]
2. 16, 19, 27, 10, 5, 7, 12, 15       [ 13.5 ]

2. Calculate the median of the following distribution:

xi:	15	20	25	30	35	40	45	50
fi:	7	15	19	23	20	15	8	5

[ Answer: 30 ]

3. Find the median for the following data representing heights of 45 students.

Ht. in cms:	158-162	162-166	166-170	170-174	174-178	178-182
No. of students:	3	7	12	15	6	2

[ Answer: 170.13 cms ]

4. Calculate the median wage for the following data:

Wages in Rs.:	Less than 35	35 – 40	40 – 45	45 – 50	Over 50
No. of workers:	24	62	99	18	15

[ Rs.41.16 ]

5. For the following data, find the median age.

Age in years:	Below 35	35 – 50	50 – 65	65 – 80	Above 80
No. of persons:	20	18	32	18	12

[ 55.625 years ]

6. Find the median and the two quartiles for the following data.  

Rainfall in cms:	20-25	25-30	30-35	35-40	40-45	45-50	50-55
No. of Years:	2	5	8	12	10	7	6

[ Median = 39.17,   Q1 = 33.44  and  Q3 = 45.36 ]

7. For the following distribution of weights of 60 students, find the three quartiles.

Weights in Kgs:	30-34	35-39	40-44	45-49	50-54	55-59	60-64
No. of students:	3	5	12	18	14	6	2

[ Median = 47.28,   Q1 = 42.42  and  Q3 = 52 ]

8. For the following distribution of weights of 60 students, find the three quartiles.

Commission in Rs.	100-140	140-180	180-200	200-220	220-240	240-260	260-300
No. of Salesmen:	14	45	52	80	32	23	24

[ Median = 206,   Q1 = 183.27  and  Q3 = 227.19 ]

9. The median marks of 100 students in Accountancy are 56.  It was later found that marks of one student were wrongly considered as 76 instead of 67.  What would be the correct median? [ Median is unaltered ]

10. In a batch of 25 students, 10 students failed in a test, by obtaining less than 35 marks.  Those who passed the test got 40, 45, 57, 60, 49, 52, 75, 72, 80, 87, 55, 58, 65, and 60 marks.  What was the median of the marks of all the 25 students?   [ 45 ]

11. In a group of 25 children the median height is 164 cms and the heights of the tallest and shortest boy in the group are 170 cms and 154 cms respectively.  To this group 4 children are added with the heights 152, 150, 174,  and  171 cms.  Find the median height of the new group of 29 children.  [ 164 cms. ]

12. If the median height for the following distribution is 162.5 cms, find the missing frequency.

Height in cms:	150 – 155	155 – 160	160 – 165	165 – 170	170 – 175	175 – 180
No. of students:	3	6	8	…	3	1

[ Answer: 5 ]

13.   If the median marks are 43.25, find the missing frequency:

Age in years:	10-19	20-29	30-39	40-49	50-59	60-69	70-79
No. of Persons:	2	5	10	8	…	5	3

[ Answer: 7 ]

14. If the median for the following distribution is Rs.26.25, find the missing frequency.

Wages in Rs.:	No. of persons
12.5 – 17.5 17.5 – 22.5 22.5 – 27.5 27.5 – 32.5 32.5 – 37.5 37.5 – 42.5 42.5 – 47.5 47.5 – 52.5 52.5 – 57.5	2 22 10 … 3 4 6 1 1	[ 16 ]
Total	63

15. If the median marks in History for a group of students are 27, find the number of students getting marks between 30 and 40.

Marks:	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
No. of Students:	5	5	10	…	3

[ Answer: 11 ]

16. The following data represents the weekly wages in Rs.  of a group of workers.  If the median is Rs.114, find the missing frequency.

Weekly wages in Rs.	60-75	75-90	90-105	105-120	120-135	135-150
No. of workers:	3	3	6	5	…	6

[ Answer : 7 ]

17. If the first and the third quartiles for the following distribution are given to be 23.125 and 43.5 respectively, find the missing frequencies.

Weekly wages in Rs.	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60
No. of workers:	5	…	20	30	…	10

[ Answer: 15 & 25 ]

18. Find the missing frequencies given that the first quartile is 320 and the third quartile is 550.

Weekly wages in Rs.	100-200	200-300	300-400	400-500	500-600	600-700
No. of workers:	7	10	…	20	16	…

[ Answer: 15 & 12 ]

19. If the median of the following distribution is 146 and the total of the frequencies is 229, find the missing frequencies.

C.I.:	110-120	120-130	130-140	140-150	150-160	160-170	170-180
Frequency:	12	…	34	65	46	…	18

[ Answer: 30 & 25 ]

20. An incomplete distribution is given below:

C.I.:	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Frequency:	13	30	…	65	…	25	18

You are given that the median value is 46 and the total number of frequencies is 230.  Also calculate the mean of the completed data.

[ Answer: 34 & 45 and the mean value = 45.83 ]

MODE

Mode is that value of the variable, which characterizes more items than any other value.  It is the value of greatest frequency or more precisely greatest frequency density.  Mode cannot be calculated unless the data are converted in the form of a discrete or a continuous distribution.  In some distributions it is difficult to get the exact value of mode as observations may concentrate around two or more values.  In such cases the distribution s bimodal, trimodal or multimodal.

Mode is a measure which should be used with caution, only when the person believes that it has relevance.  The mode can occur at an extreme value, in which vase it will be a poor measure or central tendency.  

Example:

Find the mode of the following data:

21, 44, 31, 21, 57, 36, 21, 44, 45, 21

On observing the given data, we see that the value 21 occurs 4 times which is the maximum.  Hence mode = 21.

In the case of frequency distribution, Mode is calculated using the following formula:

Where  is the lower limit of the C.I. of the modal class

 is the upper limit of the C.I. of the modal class.

 is the difference between the frequency at the mode class & the previous one

 is the difference between the frequency at the mode class & the next one.

c   is the length or the width of the C.I.

PROBLEMS:

1. Calculate the value of mode from the following data:

Income in Rs.	200 – 400	400 – 600	600 – 800	800-1000	1000-1200
No. of persons:	16	34	60	37	13

[ Answer: Rs.706.12 ]

2. The following data gives the consumption of electricity.  Calculate the value of mode.

No. of Units:	0 -100	100-200	200-300	300-400	400-500	500-600
No. of consumers:	9	18	35	32	28	10

[ Answer: 285 units ]

3. The following are the marks in a test.  Find the mode.  

Marks:	10-30	30-50	50-70	70-90	90-110	110-130
No. of students:	4	10	14	12	8	6

[ Answer: 63.3 ]

4. Calculate the modal wages for the following distribution:

Wages in Rs.:	10-15	15-20	20-25	25-30	30-35	35-40
No. of Employees:	3	5	15	20	8	7

[ Answer: Rs. 26.47 ]

5. If the mode for the following distribution is 130, find the missing frequency.

Class Interval:	60-75	75-90	90-105	105-120	120-135	135-150
Frequency:	3	3	6	…	7	6

[ Answer: 5 ]

6 If the mode of the following data is 750 and the total of the frequencies is 186, find the missing frequencies.

Life in hrs.:	200-400	400-600	600-800	800-1000	1000-1200	1200-1400	1400-1600
No. of bulbs:	10	…	50	45	30	…	5

[ Answer: 35 & 11 ]

7. Prove that the value of median lies between mean and mode using the following data.

Age (below)	10	20	30	40	50	60
No. of persons:	11	35	50	79	89	100

[ Answer: Mean = 28.6, Median = 30, Mode = 34.24 ]

8. Find the mean, median and mode for the following data.

Class Interval:	60-75	75-90	90-105	105-120	120-135	135-150
Frequency:	3	3	6	5	7	6

[ Answer: Mean = 111.15, Median = 114, Mode = 130 ]

9. Find the mean, median and mode for the following data.

Class Interval:	10-30	30-50	50-70	70-90	90-110	110-130
Frequency:	4	10	14	12	8	6

[ Answer: Mean = 70.37, Median = 68.57, Mode = 63.33 ]

10. If the median and mode of the following distribution are 33.5 and 34 respectively, find the missing frequencies.

Wages in Rs.:	0-10	10-20	20-30	30-40	40-50	50-60	60-70	Total
No. of Workers:	4	16	…	…	…	6	4	230

[ Answer: 60, 100 and 40 ]

11. Given that the mean of wages is Rs.418.75 and the mode is Rs.362.50, find the missing frequencies.  Hence calculate the median of the completed data.

Wages in Rs.:	100-200	200-300	300-400	400-500	500-600	600-700
No. of Workers:	5	12	…	…	14	11

[ Answer:  22,  16  and  Median = 406.25 ]

12. Find the missing frequencies for the following data, given that the modal marks are 53.25 and median is 52.5.  Find the arithmetic mean of the completed data.

Marks:	20-29	30-39	40-49	50-59	60-69	70-79	80-89
No. of Students:	10	18	25	…	15	12	…

[ Answer: 40, 10 and 52.8076 ]

13. Find the missing frequencies for the following data given that the mode of the distribution is 44 and the median is 45.8

Age in years:	10-20	20-30	30-40	40-50	50-60	60-70	70-80	80-90
No. of persons:	10	10	…	50	29	15	…	10

[ Answer: 36 and 10 ]

14. Find the missing frequencies if the mode of the following distribution is given to be 95 and arithmetic mean 96.

Weekly Expenditure:	50 – 70	70 – 90	90 – 110	110 – 130	130 – 150
No. of Families:	…	60	70	…	10

[ Answer: 20 and 40 ]

15. The following data gives the distribution of marks of some students.  The arithmetic mean of marks is 78 and the mode is 75.  Find the missing frequencies.

Marks:	10-30	30-50	50-70	70-90	90-110	110-130	130-150
No. of students:	5	…	25	30	…	10	5

[ Answer: 10 and 15 ]

16. The median age of the following distribution is 44 years.  The modal age is 43 years.  Two of the frequencies however are missing.  Find those frequencies given the following data.

Age in years:	25-30	30-35	35-40	40-45	45-50	50-55	55-60
No.of persons:	8	…	24	30	…	20	14

[ Answer: 10 and 26 ]

17. Find the missing frequencies given that the median and mode of the distribution are 1504 and 1500 respectively.

Life in hours:	950-1150	1150-1350	1350-1550	1550-1750	1750-1950	1950-2150
No. of bulbs:	..	43	100	…	23	13

[ Answer: 20 and 81 ]

18. The first and the third quartiles of the following data are given to be 12.5 marks and 25 marks respectively.  Find the missing frequencies.

Marks:	0-5	5-10	10-15	15-20	20-25	25-30	30-35	35-40	Total
Frequency:	4	8	…	19	…	10	5	…	72

[ Answer: 12, 11 and 3 ]

19. Find the missing frequencies given that the mode is 4400 hours and arithmetic mean is 4100 hours.

Life in hours:	1000-2000	2000-3000	3000-4000	4000-5000	5000-6000	6000-7000	7000-8000
No. of bulbs:	100	…	200	…	150	50	50

[ Answer: 150 and 300 ]

20. If the arithmetic mean for the following frequency distribution is 54 years, find the missing frequency and also calculate its mode and median.

Age in years:	0 – 20	20 – 40	40 – 60	60 – 80	80 – 100
No. of persons:	4	5	…	11	5

[ Answer: 15, 54.29 years and 54.67 years ]