Chapter 1: Mathematical Logic
Exercise 1.1
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board
EXERCISE 1.1Q 1 PAGE 2
Exercise 1.1 | Q 1 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
A triangle has ‘n’ sides
SOLUTION
It is an open sentence. Hence, it is not a statement.
[Note: Answer given in the textbook is ‘it is a statement’. However, we found that ‘It is not a statement’.]
EXERCISE 1.1Q 2 PAGE 2
Exercise 1.1 | Q 2 | Page 2
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The sum of interior angles of a triangle is 180°
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 3 PAGE 2
Exercise 1.1 | Q 3 | Page 2
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
You are amazing!
SOLUTION
It is an exclamatory sentence. Hence, it is not a statement.
EXERCISE 1.1Q 4 PAGE 2
Exercise 1.1 | Q 4 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
Please grant me a loan.
SOLUTION
It is a request. Hence, it is not a statement.
EXERCISE 1.1Q 5 PAGE 2
Exercise 1.1 | Q 5 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
√-4 is an irrational number.
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
EXERCISE 1.1Q 6 PAGE 2
Exercise 1.1 | Q 6 | Page 2
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
x2 − 6x + 8 = 0 implies x = −4 or x = −2.
SOLUTION
It is a statement which is false. Hence, it’s truth value if F.
EXERCISE 1.1Q 7 PAGE 3
Exercise 1.1 | Q 7 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
He is an actor.
SOLUTION
It is an open sentence. Hence, it is not a statement.
EXERCISE 1.1Q 8 PAGE 3
Exercise 1.1 | Q 8 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
Did you eat lunch yet?
SOLUTION
It is an interrogative sentence. Hence, it is not a statement.
EXERCISE 1.1Q 9 PAGE 3
Exercise 1.1 | Q 9 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Have a cup of cappuccino.
SOLUTION
It is an imperative sentence, hence it is not a statement.
EXERCISE 1.1Q 10 PAGE 3
Exercise 1.1 | Q 10 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
(x + y)2 = x2 + 2xy + y2 for all x, y ∈ R.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 11 PAGE 3
Exercise 1.1 | Q 11 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
Every real number is a complex number.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 12 PAGE 3
Exercise 1.1 | Q 12 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
1 is a prime number.
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
EXERCISE 1.1Q 13 PAGE 3
Exercise 1.1 | Q 13 | Page 3
State which of the following sentences is a statement. Justify your answer if it is a statement. Write down its truth value.
With the sunset the day ends.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 14 PAGE 3
Exercise 1.1 | Q 14 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
1 ! = 0
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
[Note: Answer in the textbook is incorrect]
EXERCISE 1.1Q 15 PAGE 3
Exercise 1.1 | Q 15 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
3 + 5 > 11
SOLUTION
It is a statement which is false. Hence, it’s truth value is F.
EXERCISE 1.1Q 16 PAGE 3
Exercise 1.1 | Q 16 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The number π is an irrational number.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
[Note: Answer in the textbook is incorrect]
EXERCISE 1.1Q 17 PAGE 3
Exercise 1.1 | Q 17 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
x2 - y2 = (x + y)(x - y) for all x, y ∈ R.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 18 PAGE 3
Exercise 1.1 | Q 18 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The number 2 is the only even prime number.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 19 PAGE 3
Exercise 1.1 | Q 19 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Two co-planar lines are either parallel or intersecting.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 20 PAGE 3
Exercise 1.1 | Q 20 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
The number of arrangements of 7 girls in a row for a photograph is 7!.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 21 PAGE 3
Exercise 1.1 | Q 21 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Give me a compass box.
SOLUTION
It is an imperative sentence. Hence, it is not a statement.
EXERCISE 1.1Q 22 PAGE 3
Exercise 1.1 | Q 22 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Bring the motor car here.
SOLUTION
It is an imperative sentence. Hence, it is not a statement.
EXERCISE 1.1Q 23 PAGE 3
Exercise 1.1 | Q 23 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
It may rain today.
SOLUTION
It is an open sentence. Hence, it is not a statement.
EXERCISE 1.1Q 24 PAGE 3
Exercise 1.1 | Q 24 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
If a + b < 7, where a ≥ 0 and b ≥ 0 then a < 7 and b < 7.
SOLUTION
It is a statement which is true. Hence, it’s truth value is T.
EXERCISE 1.1Q 25 PAGE 3
Exercise 1.1 | Q 25 | Page 3
State which of the following sentence is a statement. Justify your answer if it is a statement. Write down its truth value.
Can you speak in English?
SOLUTION
It is an interrogative sentence. Hence, it is not a statement.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.2 [Page 6]
EXERCISE 1.2Q 1.1 PAGE 6
Express the following statement in symbolic form.
e is a vowel or 2 + 3 = 5
SOLUTION
Let p : e is a vowel.
q : 2 + 3 = 5
The symbolic form is p ∨ q.
EXERCISE 1.2Q 1.2 PAGE 6
Express the following statement in symbolic form.
Mango is a fruit but potato is a vegetable.
SOLUTION
Let p : Mango is a fruit.
q : Potato is a vegetable.
The symbolic form is p Λ q.
EXERCISE 1.2Q 1.3 PAGE 6
Express the following statement in symbolic form.
Milk is white or grass is green.
SOLUTION
Let p : Milk is white.
q : Grass is green.
The symbolic form is p ∨ q.
EXERCISE 1.2Q 1.4 PAGE 6
Express the following statement in symbolic form.
I like playing but not singing.
SOLUTION
Let p : I like playing.
q : I do not like singing.
The symbolic form is p ∧ q.
EXERCISE 1.2Q 1.5 PAGE 6
Express the following statement in symbolic form.
Even though it is cloudy, it is still raining.
SOLUTION
Let p : It is cloudy.
q : It is still raining.
The symbolic form is p ∧ q.
EXERCISE 1.2Q 2.1 PAGE 6
Write the truth value of the following statement.
Earth is a planet and Moon is a star.
SOLUTION
Let p : Earth is a planet.
q : Moon is a star.
The truth values of p and q are T and F respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ F ≡ F
∴ Truth value of the given statement is F.
EXERCISE 1.2Q 2.2 PAGE 6
Write the truth value of the following statement.
16 is an even number and 8 is a perfect square.
SOLUTION
Let p : 16 is an even number.
q : 8 is a perfect square.
The truth values of p and q are T and F respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ F ≡ F
∴ Truth value of the given statement is F.
EXERCISE 1.2Q 2.3 PAGE 6
Write the truth value of the following statement.
A quadratic equation has two distinct roots or 6 has three prime factors.
SOLUTION
Let p : A quadratic equation has two distinct roots.
q : 6 has three prime factors.
The truth values of p and q are F and F respectively.
The given statement in symbolic form is p ∨ q.
∴ p ∨ q ≡ F ∨ F ≡ F
∴ Truth value of the given statement is F.
EXERCISE 1.2Q 2.4 PAGE 6
Write the truth value of the following statement.
The Himalayas are the highest mountains but they are part of India in the North East.
SOLUTION
Let p : Himalayas are the highest mountains.
q : Himalayas are the part of India in the north east.
The truth values of p and q are T and T respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ T ≡ T
∴ Truth value of the given statement is T.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.3 [Page 7]
EXERCISE 1.3Q 1.1 PAGE 7
Write the negation of the following statement.
All men are animals.
SOLUTION
Some men are not animals.
EXERCISE 1.3Q 1.2 PAGE 7
Write the negation of the following statement.
− 3 is a natural number.
SOLUTION
– 3 is not a natural number.
EXERCISE 1.3Q 1.3 PAGE 7
Write the negation of the following statement.
It is false that Nagpur is capital of Maharashtra
SOLUTION
Nagpur is capital of Maharashtra.
EXERCISE 1.3Q 1.4 PAGE 7
Write the negation of the following statement.
2 + 3 ≠ 5
SOLUTION
2 + 3 = 5
EXERCISE 1.3Q 2.1 PAGE 7
Write the truth value of the negation of the following statement.
√5 is an irrational number.
SOLUTION
Truth value of the given statement is T.
∴ Truth value of its negation is F.
EXERCISE 1.3Q 2.2 PAGE 7
Write the truth value of the negation of the following statement.
London is in England.
SOLUTION
Truth value of the given statement is T.
∴ Truth value of its negation is F.
EXERCISE 1.3Q 2.3 PAGE 7
Write the truth value of the negation of the following statement.
For every x ∈ N, x + 3 < 8.
SOLUTION
Truth value of the given statement is F.
∴ Truth value of its negation is T.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.4 [Pages 10 - 11]
Write the following statement in symbolic form.
If triangle is equilateral then it is equiangular.
SOLUTION
Let p : Triangle is equilateral.
q : Triangle is equiangular.
The symbolic form is p → q.
Write the following statement in symbolic form.
It is not true that “i” is a real number.
SOLUTION
Let p : i is a real number.
The symbolic form is ~ p.
Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
SOLUTION
Let p : It is cloudy.
q : It is raining.
The symbolic form is ~p ∧ q.
Write the following statement in symbolic form.
Milk is white if and only if the sky is not blue.
SOLUTION
Let p : Milk is white.
q : Sky is blue.
The symbolic form is p ↔ ~ q.
Write the following statement in symbolic form.
Stock prices are high if and only if stocks are rising.
SOLUTION
Let p : Stock prices are high.
q : Stock are rising
The symbolic form is p ↔ q.
Write the following statement in symbolic form.
If Kutub-Minar is in Delhi then Taj-Mahal is in Agra.
SOLUTION
Let p : Kutub-Minar is in Delhi.
q : Taj-Mahal Is in Agra.
The symbolic form is p → q.
Find the truth value of the following statement.
It is not true that 3 − 7i is a real number.
SOLUTION
Let p : 3 – 7i is a real number.
The truth value of p is F.
The given statement in symbolic form is ~p.
∴ ~ p ≡ ~ F ≡ T
∴ Truth value of the given statement is T.
Find the truth value of the following statement.
If a joint venture is a temporary partnership, then discount on purchase is credited to the supplier.
SOLUTION
Let p : A joint venture is a temporary partnership. q : Discount on purchase is credited to the supplier.
The truth value of p and q are T and F respectively.
The given statement in symbolic form is p → q.
∴ p → q ≡ T → F ≡ F
∴ Truth value of the given statement is F.
Find the truth value of the following statement.
Every accountant is free to apply his own accounting rules if and only if machinery is an asset.
SOLUTION
Let p : Every accountant is free to apply his own accounting rules.
q : Machinery is an asset.
The truth values of p and q are F and T respectively.
The given statement in symbolic form is p ↔ q.
∴ p ↔ q ≡ F ↔ T ≡ F
∴ Truth value of the given statement is F.
Find the truth value of the following statement.
Neither 27 is a prime number nor divisible by 4.
SOLUTION
Let p : 27 is a prime number.
q : 27 is divisible by 4.
The truth values of p and q are F and F respectively.
The given statement in symbolic form is ~ p ∧ ~ q.
∴ ~ p ∧ ~ q ≡ ~ F ∧ ~ F ≡ T ∧ T ≡ T
∴ Truth value of the given statement is T.
Find the truth value of the following statement.
3 is a prime number and an odd number.
SOLUTION
Let p : 3 is a prime number.
q : 3 is an odd number.
The truth values of p and q are T and T respectively.
The given statement in symbolic form is p ∧ q.
∴ p ∧ q ≡ T ∧ T ≡ T
∴ Truth value of the given statement is T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
p ∧ (q ∧ r)
SOLUTION
p ∧ (q ∧ r) ≡ T ∧ (T ∧ F)
≡ T ∧ F
≡ F
Hence, truth value if F.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ∨ (r ∧ s)
SOLUTION
(p → q) ∨ (r ∧ s) ≡ (T → T) ∨ (F ∧ F)
≡ T ∨ F
≡ T
Hence, truth value if T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [(~ p ∨ s) ∧ (~ q ∧ r)]
SOLUTION
~ [(~ p ∨ s) ∧ (~ q ∧ r)] ≡ ~[(~T ∨ F) ∧ (~T ∧ F)]
≡ ~[(F ∨ F) ∧ (F ∧ F)
≡ ~ (F ∧ F)
≡ ~ F
≡ T
Hence, truth value if T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
(p → q) ↔ ~(p ∨ q)
SOLUTION
(p → q) ↔ ~(p ∨ q) ≡ (T → T) ↔ (T ∨ T)
≡ T ↔ ~ T
≡ T ↔ F
≡ F
Hence, truth value if F.
If p and q are true and r and s are false, find the truth value of the following compound statement.
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
SOLUTION
[(p ∨ s) → r] ∨ ~ [~ (p → q) ∨ s]
≡ [(T ∨ F) → F] ∨ ~[~ (T → T) ∨ F]
≡ (T → F) ∨ ~ (~ T ∨ F)
≡ F ∨ ~ (F ∨ F)
≡ F ∨ ~ F
≡ F ∨ T
≡ T
Hence, truth value is T.
If p and q are true and r and s are false, find the truth value of the following compound statement.
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
SOLUTION
~ [p ∨ (r ∧ s)] ∧ ~ [(r ∧ ~ s) ∧ q]
≡ ~ [T ∨ (F ∧ F)] ∧ ~ [(F ∧ ~ F) ∧ T]
≡ ~ (T ∨ F) ∧ ~ [(F ∧ T) ∧ T]
≡ ~ T ∧ ~ (F ∧ T)
≡ F ∧ ~ F
≡ F ∧ T
≡ F
Hence, truth value is F.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is not holiday or Ram studies on holiday.
SOLUTION
Symbolic form of the given statement is ~ p ∨~q
∴ ~ p ∨~ q ≡ ~ T ∨ ~ T
≡ F ∨ F
≡ F
Hence, truth value is F.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
If Sunday is not holiday then Ram studies on holiday.
SOLUTION
Symbolic form of the given statement is
~ p → ~ q
∴ ~ p → ~ q ≡ ~ T → ~ T
≡ F → F
≡ T
Hence, truth value is T.
Assuming that the following statement is true,
p : Sunday is holiday,
q : Ram does not study on holiday,
find the truth values of the following statements.
Sunday is a holiday and Ram studies on holiday.
SOLUTION
Symbolic form of the given statement is p ∧ ~ q
∴ p ∧ ~ q ≡ T ∧ ~ T
≡ T ∧ F
≡ F
Hence, truth value is F.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
p ↔ ~ q
SOLUTION
He swims if and only if water is not warm.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
~ (p ∨ q)
SOLUTION
It is not true that he swims or water is warm.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q → p
SOLUTION
If water is warm then he swims.
If p : He swims
q : Water is warm
Give the verbal statement for the following symbolic statement.
q ∧ ~ p
SOLUTION
Water is warm and he does not swim.
EXERCISE 1.5PAGE 12
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.5 [Page 12]
Use quantifiers to convert the following open sentences defined on N, into a true statement.
x2 + 3x - 10 = 0
SOLUTION
∃ x ∈ N, such that x2 + 3x – 10 = 0
It is true statement, since x = 2 ∈ N satisfies it.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
3x - 4 < 9
SOLUTION
∃ x ∈ N, such that 3x – 4 < 9
It is true statement, since
x = 2, 3, 4 ∈ N satisfies 3x - 4 < 9.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
n2 ≥ 1
SOLUTION
∀ n ∈ N, n2 ≥ 1
It is true statement, since all n ∈ N satisfy it.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
2n - 1 = 5
SOLUTION
∃ n ∈ N, such that 2n - 1 = 5
It is a true statement since all n = 3 ∈ N satisfy 2n - 1 = 5.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
y + 4 > 6
SOLUTION
∃ y ∈ N, such that y + 4 > 6
It is a true statement since y = 3, 4, ... ∈ N satisfy y + 4 > 6.
Use quantifiers to convert the following open sentences defined on N, into a true statement.
3y - 2 ≤ 9
SOLUTION
∃ y ∈ N, such that 3y - 2 ≤ 9
It is a true statement since y = 1, 2, 3 ∈ N satisfy it.
If B = {2, 3, 5, 6, 7} determine the truth value of ∀ x ∈ B such that x is prime number.
SOLUTION
For x = 6, x is not a prime number.
∴ x = 6 does not satisfies the given statement.
∴ The given statement is false.
∴ It’s truth value is F.
If B = {2, 3, 5, 6, 7} determine the truth value of
∃ n ∈ B, such that n + 6 > 12.
SOLUTION
For n = 7, n + 6 = 7 + 6 = 13 > 12
∴ n = 7 satisfies the equation n + 6 > 12.
∴ The given statement is true.
∴ It’s truth value is T.
If B = {2, 3, 5, 6, 7} determine the truth value of
∃ n ∈ B, such that 2n + 2 < 4.
SOLUTION
There is no n in B which satisfies 2n + 2 < 4.
∴ The given statement is false.
∴ It’s truth value is F.
If B = {2, 3, 5, 6, 7} determine the truth value of
∀ y ∈ B, such that y2 is negative.
SOLUTION
There is no y in B which satisfies y2 < 0.
∴ The given statement is false.
∴ It’s truth value is F.
If B = {2, 3, 5, 6, 7} determine the truth value of
∀ y ∈ B, such that (y - 5) ∈ N
SOLUTION
For y = 2, y – 5 = 2 – 5 = –3 ∉ N.
∴ y = 2 does not satisfies the equation (y – 5) ∈ N.
∴ The given statement is false.
∴ It’s truth value is F.
EXERCISE 1.6PAGE 16
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.6 [Page 16]
Prepare truth tables for the following statement pattern.
p → (~ p ∨ q)
SOLUTION
p → (~ p ∨ q)
| p | q | ~p | ~ p ∨ q | p → (~ p ∨ q) |
| T | T | F | T | T |
| T | F | F | F | F |
| F | T | T | T | T |
| F | F | T | T | T |
Prepare truth tables for the following statement pattern.
(~ p ∨ q) ∧ (~ p ∨ ~ q)
SOLUTION
(~ p ∨ q) ∧ (~ p ∨ ~ q)
| p | q | ~p | ~q | ~p∨q | ~p∨~q | (~p∨q)∧(~p∨~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | F |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
Prepare truth tables for the following statement pattern.
(p ∧ r) → (p ∨ ~ q)
SOLUTION
(p ∧ r) → (p ∨ ~ q)
| p | q | r | ~q | p ∧ r | p∨~q | (p ∧ r) → (p ∨ ~ q) |
| T | T | T | F | T | T | T |
| T | T | F | F | F | T | T |
| T | F | T | T | T | T | T |
| T | F | F | T | F | T | T |
| F | T | T | F | F | F | T |
| F | T | F | F | F | F | T |
| F | F | T | T | F | T | T |
| F | F | F | T | F | T | T |
Prepare truth tables for the following statement pattern.
(p ∧ q) ∨ ~ r
SOLUTION
(p ∧ q) ∨ ~ r
| p | q | r | ~r | p ∧ q | (p ∧ q) ∨ ~ r |
| T | T | T | F | T | T |
| T | T | F | T | T | T |
| T | F | T | F | F | F |
| T | F | F | T | F | T |
| F | T | T | F | F | F |
| F | T | F | T | F | T |
| F | F | T | F | F | F |
| F | F | F | T | F | T |
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
q ∨ [~ (p ∧ q)]
SOLUTION
| p | q | p ∧ q | ~ (p ∧ q) | q ∨ [~ (p ∧ q)] |
| T | T | T | F | T |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | F | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
(~ q ∧ p) ∧ (p ∧ ~ p)
SOLUTION
| p | q | ~p | ~q | (~q∧p) | (p∧~p) | (~q∧p)∧(p∧~p) |
| T | T | F | F | F | F | F |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | F |
| F | F | T | T | F | F | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
(p ∧ ~ q) → (~ p ∧ ~ q)
SOLUTION
| p | q | ~p | ~q | p∧~q | ~p∧~q | (p∧~q)→(~p∧~q) |
| T | T | F | F | F | F | T |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | T |
| F | F | T | T | F | T | T |
The truth values in the last column are not identical. Hence, it is contingency.
Examine whether the following statement pattern is a tautology, a contradiction or a contingency.
~ p → (p → ~ q)
SOLUTION
| p | q | ~p | ~q | p→~q | ~p→(p→~q) |
| T | T | F | F | F | T |
| T | F | F | T | T | T |
| F | T | T | F | T | T |
| F | F | T | T | T | T |
All the truth values in the last column are T. Hence, it is tautology.
Prove that the following statement pattern is a tautology.
(p ∧ q) → q
SOLUTION
| p | q | p ∧ q | (p∧q)→q |
| T | T | T | T |
| T | F | F | T |
| F | T | F | T |
| F | F | F | T |
All the truth values in the last column are T. Hence, it is tautology.
Prove that the following statement pattern is a tautology.
(p → q) ↔ (~ q → ~ p)
SOLUTION
| p | q | ~p | ~q | p→q | ~q→~p | (p→q)↔(~q→~p) |
| T | T | F | F | T | T | T |
| T | F | F | T | F | F | T |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Prove that the following statement pattern is a tautology.
(~p ∧ ~q ) → (p → q)
SOLUTION
| p | q | ~p | ~q | ~p∧~q | p→q | (~p∧~q)→(p→q) |
| T | T | F | F | F | T | T |
| T | F | F | T | F | F | T |
| F | T | T | F | F | T | T |
| F | F | T | T | T | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Prove that the following statement pattern is a tautology.
(~ p ∨ ~ q) ↔ ~ (p ∧ q)
SOLUTION
| p | q | ~p | ~q | ~p∨~q | p∧q | ~p∨~q | (~p∨~q↔~(p ∧ q) |
| T | T | F | F | F | T | F | T |
| T | F | F | T | T | F | T | T |
| F | T | T | F | T | F | T | T |
| F | F | T | T | T | F | T | T |
All the truth values in the last column are T. Hence, it is a tautology.
Prove that the following statement pattern is a contradiction.
(p ∨ q) ∧ (~p ∧ ~q)
SOLUTION
| p | q | ~p | ~q | p∨q | ~p∧~q | (p∨q)∧(~p∧~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | T | F | F |
| F | T | T | F | T | F | F |
| F | F | T | T | F | T | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Prove that the following statement pattern is a contradiction.
(p ∧ q) ∧ ~p
SOLUTION
| p | q | ~p | p∧q | (p∧q)∧~p |
| T | T | F | T | F |
| T | F | F | F | F |
| F | T | T | F | F |
| F | F | T | F | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Prove that the following statement pattern is a contradiction.
(p ∧ q) ∧ (~p ∨ ~q)
SOLUTION
| p | q | ~p | ~q | p∧q | ~p∨~q | (p∧q)∧(~p∨~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | F |
| F | T | T | F | F | T | F |
| F | F | T | T | F | T | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Prove that the following statement pattern is a contradiction.
(p → q) ∧ (p ∧ ~ q)
SOLUTION
| p | q | ~q | p→q | p∧~q | (p→q)∧(p∧~q) |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| F | T | F | T | F | F |
| F | F | T | T | F | F |
All the truth values in the last column are F. Hence, it is a contradiction.
Show that the following statement pattern is contingency.
(p∧~q) → (~p∧~q)
SOLUTION
| p | q | ~p | ~q | p∧~q | ~p∧~q | (p∧~q)→(~p∧~q) |
| T | T | F | F | F | F | T |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | T |
| F | F | T | T | F | T | T |
The truth values in the last column are not identical. Hence, it is contingency.
Show that the following statement pattern is contingency.
(p → q) ↔ (~ p ∨ q)
SOLUTION
| p | q | ~p | p→q | ~p∨q | (p→q)↔(~p∨q) |
| T | T | F | T | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | F | T | T | T | T |
All the truth values in the last column are T. Hence, it is a tautology. Not contingency.
Show that the following statement pattern is contingency.
p ∧ [(p → ~ q) → q]
SOLUTION
| p | q | ~q | p→~q | (p→~q)→q | p∧[(p→~q)→q] |
| T | T | F | F | T | T |
| T | F | T | T | F | F |
| F | T | F | T | T | F |
| F | F | T | T | F | F |
Truth values in the last column are not identical. Hence, it is contingency.
Show that the following statement pattern is contingency.
(p → q) ∧ (p → r)
SOLUTION
| p | q | r | p→q | p→r | (p→q)∧(p→r) |
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| T | F | F | F | F | F |
| F | T | T | T | T | T |
| F | T | F | T | T | T |
| F | F | T | T | T | T |
| F | F | F | T | T | T |
The truth values in the last column are not identical. Hence, it is contingency.
Exercise 1.6 | Q 6.1 | Page 16
Using the truth table, verify
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | q∧r | p∨(q∧r) | p∨q | p∨r | (p∨q)∧(p∨r) |
| T | T | T | T | T | T | T | T |
| T | T | F | F | T | T | T | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | T | T | T | T | T |
| F | T | F | F | F | T | F | F |
| F | F | T | F | F | F | T | F |
| F | F | F | F | F | F | F | F |
The entries in columns 5 and 8 are identical.
∴ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Using the truth table, verify
p → (p → q) ≡ ~ q → (p → q)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | ~q | p→q | p→(p→q) | ~q→(p→q) |
| T | T | F | T | T | T |
| T | F | T | F | F | F |
| F | T | F | T | T | T |
| F | F | T | T | T | T |
In the above truth table, entries in columns 5 and 6 are identical.
∴ p → (p → q) ≡ ~ q → (p → q)
Using the truth table, verify
~(p → ~q) ≡ p ∧ ~ (~ q) ≡ p ∧ q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | ~q | p→~q | ~(p→~q) | ~(~q) | p∧~(~q) | p∧q |
| T | T | F | F | T | T | T | T |
| T | F | T | T | F | F | F | F |
| F | T | F | T | F | T | F | F |
| F | F | T | T | F | F | F | F |
In the above table, entries in columns 5, 7, and 8 are identical.
∴ ~(p → ~q) ≡ p ∧ ~ (~ q) ≡ p ∧ q
Using the truth table, verify
~(p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | ~p | (p∨q) | ~(p∨q) | ~p∧q | ~(p∨q)∨(~p∧q) |
| T | T | F | T | F | F | F |
| T | F | F | T | F | F | F |
| F | T | T | T | F | T | T |
| F | F | T | F | T | F | T |
In the above truth table, the entries in columns 3 and 7 are identical.
∴ ~(p ∨ q) ∨ (~ p ∧ q) ≡ ~ p
Exercise 1.6 | Q 7.1 | Page 16
Using the truth table, verify
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | q∧r | p∨(q∧r) | p∨q | p∨r | (p∨q)∧(p∨r) |
| T | T | T | T | T | T | T | T |
| T | T | F | F | T | T | T | T |
| T | F | T | F | T | T | T | T |
| T | F | F | F | T | T | T | T |
| F | T | T | T | T | T | T | T |
| F | T | F | F | F | T | F | F |
| F | F | T | F | F | F | T | F |
| F | F | F | F | F | F | F | F |
The entries in columns 5 and 8 are identical.
∴ ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
Prove that the following pair of statement pattern is equivalent.
p ↔ q and (p → q) ∧ (q → p)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | p↔q | p→q | q→p | (p→q)∧(q→p) |
| T | T | T | T | T | T |
| T | F | F | F | T | F |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
In the above table, entries in columns 3 and 6 are identical.
∴ Statement p ↔ q and (p → q) ∧ (q → p) are equivalent.
Prove that the following pair of statement pattern is equivalent.
p → q and ~ q → ~ p and ~ p ∨ q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | ~p | ~q | p→q | ~q→~p | ~p∨q |
| T | T | F | F | T | T | T |
| T | F | F | T | F | F | F |
| F | T | T | F | T | T | T |
| F | F | T | T | T | T | T |
In the above table, entries in columns 5, 6 and 7 are identical.
∴ Statement p → q and ~q → ~p and ~p ∨ q are equivalent.
Prove that the following pair of statement pattern is equivalent.
~(p ∧ q) and ~p ∨ ~q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | ~p | ~q | p∧q | ~(p∧q) | ~p∨~q |
| T | T | F | F | T | F | F |
| T | F | F | T | F | T | T |
| F | T | T | F | F | T | T |
| F | F | T | T | F | T | T |
In the above table, entries in columns 6 and 7 are identical.
∴ Statement ~(p ∧ q) and ~p ∨ ~q are equivalent.
EXERCISE 1.7PAGE 17
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.7 [Page 17]
Write the dual of the following:
(p ∨ q) ∨ r
SOLUTION
(p ∧ q) ∧ r
Write the dual of the following:
~(p ∨ q) ∧ [p ∨ ~ (q ∧ ~ r)]
SOLUTION
~(p ∧ q) ∨ [p ∧ ~ (q ∨ ~ r)]
Write the dual of the following:
p ∨ (q ∨ r) ≡ (p ∨ q) ∨ r
SOLUTION
p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r
Write the dual of the following:
~(p ∧ q) ≡ ~ p ∨ ~ q
SOLUTION
~(p ∨ q) ≡ ~ p ∧ ~ q
Write the dual statement of the following compound statement.
13 is a prime number and India is a democratic country.
SOLUTION
13 is a prime number or India is a democratic country.
Write the dual statement of the following compound statement.
Karina is very good or everybody likes her.
SOLUTION
Karina is very good and everybody likes her.
Write the dual statement of the following compound statement.
Radha and Sushmita cannot read Urdu.
SOLUTION
Radha or Sushmita cannot read Urdu.
Write the dual statement of the following compound statement.
A number is a real number and the square of the number is non-negative.
SOLUTION
A number is a real number or the square of the number is non-negative.
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.8 [Page 21]
Write the negation of the following statement.
All the stars are shining if it is night.
SOLUTION
Let q : All stars are shining.
p : It is night.
The given statement in symbolic form is p → q. It’s negation is ~ (p → q) ≡ p ∧ ~ q
∴ The negation of a given statement is ‘It is night and some stars are not shining’.
Write the negation of the following statement.
∀ n ∈ N, n + 1 > 0
SOLUTION
∃ n ∈ N such that n + 1 ≤ 0.
Write the negation of the following statement.
∃ n ∈ N, (n2 + 2) is odd number.
SOLUTION
∀ n ∈ N, (n2 + 2) is not odd number.
Write the negation of the following statement.
Some continuous functions are differentiable.
SOLUTION
All continuous functions are not differentiable.
Using the rules of negation, write the negation of the following:
(p → r) ∧ q
SOLUTION
~ [(p → r) ∧ q] ≡ ~(p → r) ∨ ~q ....[Negation of conjunction]
≡ (p ∧ ~ r) ∨ ~q .....[Negation of implication]
Using the rules of negation, write the negation of the following:
~(p ∨ q) → r
SOLUTION
~[~(p ∨ q) → r] ≡ ~(p ∨ q) ∧ ~r ....[Negation of implication]
≡ (~p ∧ ~q) ∧ ~r .....[Negation of disjunction]
Using the rules of negation, write the negation of the following:
(~p ∧ q) ∧ (~q ∨ ~r)
SOLUTION
~[(~p ∧ q) ∧ (~q ∨ ~r)]
≡ ~(~ p ∧ q) ∨ ~ (~ q ∨ ~r) ...[Negation of conjunction]
≡ [~(~ p) ∨ ~ q] ∨ [~(~q) ∧ ~(~r)] ...[Negation of conjunction and disjunction]
≡ (p ∨ ~q) ∨ (q ∨ r) .....[Negation on negation]
Write the converse, inverse, and contrapositive of the following statement.
If it snows, then they do not drive the car.
SOLUTION
Let p : It snows.
q : They do not drive the car.
∴ The given statement is p → q.
Its converse is q → p.
If they do not drive the car then it snows.
Its inverse is ~p → ~q.
If it does not snow then they drive the car.
Its contrapositive is ~q → ~p.
If they drive the car then it does not snow.
Write the converse, inverse, and contrapositive of the following statement.
If he studies, then he will go to college.
SOLUTION
Let p : He studies.
q : He will go to college.
∴ The given statement is p → q.
Its converse is q → p.
If he will go to college then he studies.
Its inverse is ~p → ~q.
If he does not study then he will not go to college.
Its contrapositive is ~q → ~p.
If he will not go to college then he does not study.
With proper justification, state the negation of the following.
(p → q) ∨ (p → r)
SOLUTION
~[(p → q) ∨ (p → r)]
≡ ~(p → q) ∧ ~(p → r) ...[Negation of disjunction]
≡ (p ∧ ~ q) ∧ (p ∧ ~r) ....[Negation of implication]
With proper justification, state the negation of the following.
(p ↔ q) ∨ (~q → ~r)
SOLUTION
~[(p ↔ q) ∨ (~q → ~r)]
≡ ~(p ↔ q) ∧ (~q → ~r) ....[Negation of disjunction]
≡ [(p ∧ ~q) ∨ (q ∧ ~p)] ∧ ~(~q → ~r) ....[Negation of double implication]
≡ [(p ∧ ~q) ∨ (q ∧ ~p)] ∧ [~ q ∧ ~(~r)] ....[Negation of implication]
≡ [(p ∧ ~q) ∨ (q ∧ ~p)] ∧ (~ q ∧ r) ....[Negation of negation]
With proper justification, state the negation of the following.
(p → q) ∧ r
SOLUTION
~[(p → q) ∧ r]
≡ ~ (p → q) ∨ ~ r ....[Negation of conjunction]
≡ (p ∧ ~q) ∨ ~ r ....[Negation of implication]
EXERCISE 1.9PAGE 22
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.9 [Page 22]
Without using truth table, show that
p ↔ q ≡ (p ∧ q) ∨ (~p ∧ ~q)
SOLUTION
L.H.S.
≡ p ↔ q
≡ (p → q) ∧ (q → p)
≡ (~p ∨ q) ∧ (~q ∨ p)
≡ [~ p ∧ (~ q ∨ p)] ∨ [q ∧ (~ q ∨ p)] ....[Distributive law]
≡ [(~ p ∧ ~ q) ∨ (~ p ∧ p)] ∨ [(q ∧ ~ q) ∨ (q ∧ p)] .....[Distributive Law]
≡ [(~ p ∧ ~ q) ∨ F] ∨ [F ∨ (q ∧ p)] ....[Complement Law]
≡ (~ p ∧ ~ q) ∨ (q ∧ p) ....[Identity Law]
≡ (p ∧ q) ∨ (~ p ∧ ~ q) ....[Commutative Law]
≡ R.H.S.
Without using truth table, show that
p ∧ [(~ p ∨ q) ∨ ~ q] ≡ p
SOLUTION
L.H.S.
≡ p ∧ [(~ p ∨ q) ∨ ~ q]
≡ p ∧ [(~ p ∨ (q ∨ ~ q)] .....[Associative law]
≡ p ∧ (~ p ∨ T) .....[Complement law]
≡ p ∧ T .....[Identity law]
≡ p .....[Identity law]
≡ R.H.S.
Without using truth table, show that
~ [(p ∧ q) → ~ q] ≡ p ∧ q
SOLUTION
L.H.S.
≡ ~ [(p ∧ q) → ~ q]
≡ (p ∧ q) ∧ ~ (~ q) ....[Negation of implication]
≡ (p ∧ q) ∧ q .....[Negation of a negation]
≡ p ∧ (q ∧ q) ....[Associative law]
≡ p ∧ q .....[Identity law]
≡ R.H.S.
Without using truth table, show that
~r → ~ (p ∧ q) ≡ [~ (q → r)] → ~ p
SOLUTION
L.H.S.
≡ ~r → ~ (p ∧ q)
≡ ~(~ r) ∨ ~ (p ∧ q) ....[p → q ≡ ~ p ∨ q]
≡ r ∨ ~(p ∧ q) ....[Negation of negation]
≡ r ∨ (~p ∨ ~q) ....[De Morgan’s law]
≡ ~p ∨ (~q ∨ r) .....[Commutative and associative law]
≡ ~p ∨ (q → r) ....[p → q ≡ ~ p ∨ q]
≡ (q → r) ∨ ~p ......[Commutative law]
≡ ~[~ (q → r)] ∨ ~ p ......[Negation of negation]
≡ [~ (q → r)] → ~ p .....[p → q ≡ ~ p ∨ q]
= R.H.S.
Without using truth table, show that
(p ∨ q) → r ≡ (p → r) ∧ (q → r)
SOLUTION
L.H.S.
≡ (p ∨ q) → r
≡ ~ (p ∨ q) ∨ r ....[p → q → ~ p ∨ q]
≡ (~ p ∧ ~ q) ∨ r ....[De Morgan’s law]
≡ (~ p ∨ r) ∧ (~ q ∨ r) .....[Distributive law]
≡ (p → r) ∧ (q → r) .....[p → q → ~ p ∨ q]
= R.H.S.
Using the algebra of statement, prove that
[p ∧ (q ∨ r)] ∨ [~ r ∧ ~ q ∧ p] ≡ p
SOLUTION
L.H.S.
= [p ∧ (q ∨ r)] ∨ [~ r ∧ ~ q ∧ p]
≡ [p ∧ (q ∨ r)] ∨ [(~ r ∧ ~ q)∧ p] ...[Associative Law]
≡ [p ∧ (q ∨ r)] ∨ [(~q ∧ ~r) ∧ p] ....[Commutative Law]
≡ [p ∧ (q ∨ r)] ∨ [~ (q ∨ r) ∧ p] ....[De Morgan’s Law]
≡ [p ∧ (q ∨ r)] ∨ [p ∧ ~(q ∨ r)] .....[Commutative Law]
≡ p ∧ [(q ∨ r) ∨ ~(q ∨ r)] ....[Distributive Law]
≡ p ∧ t ......[Complement Law]
≡ p .....[Identity Law]
= R.H.S.
Using the algebra of statement, prove that
(p ∧ q) ∨ (p ∧ ~ q) ∨ (~ p ∧ ~ q) ≡ (p ∨ ~ q)
SOLUTION
L.H.S.
= (p ∧ q) ∨ (p ∧ ~ q) ∨ (~ p ∧ ~ q)
≡ (p ∧ q) ∨ [(p ∧ ~ q) ∨ (~ p ∧ ~ q)] ....[Associative Law]
≡ (p ∧ q) ∨ [(~q ∧ p) ∨ (~ q ∧ ~ p)] ....[Commutative Law]
≡ (p ∧ q) ∨ [~q ∧ (p ∨ ~ p)] ....[Distributive Law]
≡ (p ∧ q) ∨ (~q ∧ t) .....[Complement Law]
≡ (p ∧ q) ∨ (~q) .....[Identity Law]
≡ (p ∨ ~ q) ∧ (q ∨ ~q) .....[Distributive Law]
≡ (p ∨ ~ q) ∧ t ....[Complement Law]
≡ p ∨ ~ q .....[Identity Law]
= R.H.S.
Using the algebra of statement, prove that
SOLUTION
(p ∨ q) ∧ (~ p ∨ ~ q) ≡ (p ∧ ~ q) ∨ (~ p ∧ q)
L.H.S.
= (p ∨ q) ∧ (~ p ∨ ~ q)
≡ [(p ∨ q) ∧ ~ p] ∨ [(p ∨ q) ∧ ~ q] .....[Distributive law]
≡ [(p ∧ ~ p) ∨ (q ∧ ~ p)] ∨ [(p ∧ ~ q) ∨ (q ∧ ~ q)] .....[Distributive law]
≡ [F ∨ (q ∧ ~p)] ∨ [(p ∧ ~ q) ∨ F] .....[Complement law]
≡ (q ∧ ~p) ∨ (p ∧ ~ q) .....[Identity law]
≡ (p ∧ ~ q) ∨ (~ p ∧ q) ....[Commutative law]
= R.H.S.
EXERCISE 1.10PAGES 22 - 27
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Exercise 1.10 [Pages 22 - 27]
Represent the truth of the following statement by the Venn diagram.
Some hardworking students are obedient.
SOLUTION
Let U : The set of all students.
H : The set of all hardworking students.
O : The set of all obedient students.
Represent the truth of the following statement by the Venn diagram.
No circles are polygons.
SOLUTION
Let U : The set of all closed geometrical figures in plane.
P : The set of all polygons
C : The set of all circles.
The above Venn diagram represents truth of the given statement, P ∩ C ≠ φ
Represent the truth of the following statement by the Venn diagram.
All teachers are scholars and scholars are teachers.
SOLUTION
Let U : The set of all human beings.
T : The set of all teachers.
S : The set of all scholars
The above Venn diagram represents truth of the given statement, T = S
Represent the truth of the following statement by the Venn diagram.
If a quadrilateral is a rhombus, then it is a parallelogram.
SOLUTION
Let U : The set of all quadrilaterals.
P : The set of all parallelograms.
R : The set of all rhombuses.
The above Venn diagram represents truth of the given statement, R ⊂ P.
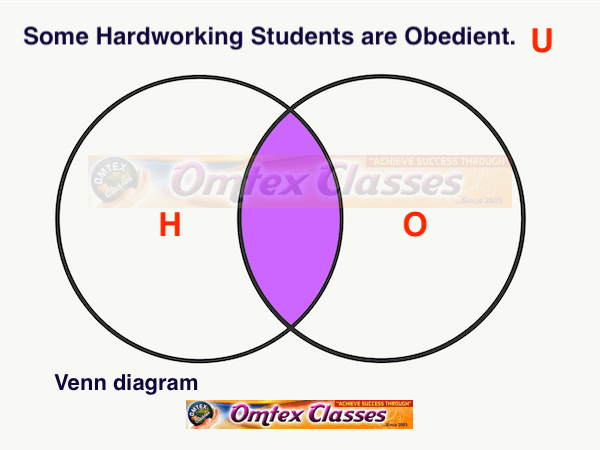
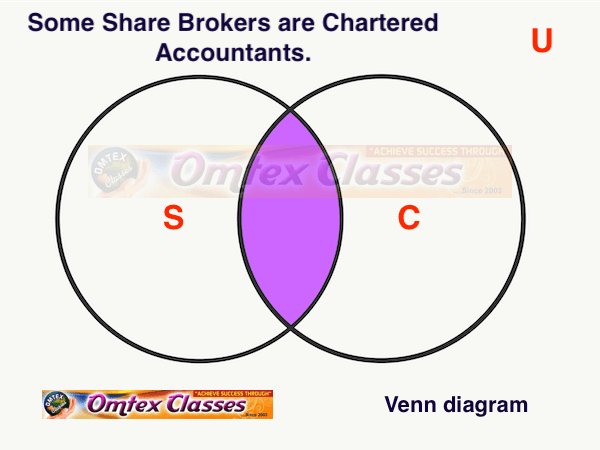
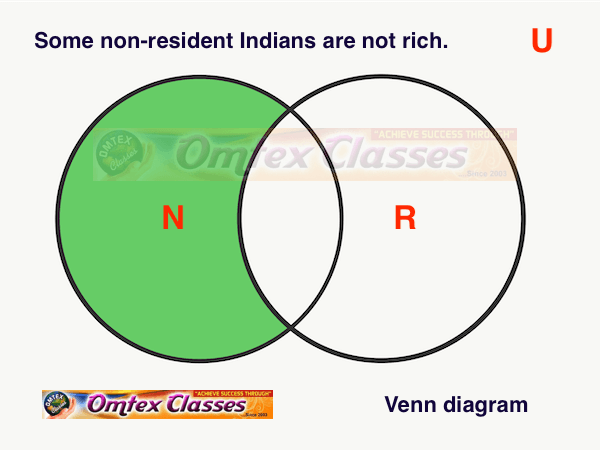
Draw a Venn diagram for the truth of the following statement.
Some share brokers are chartered accountants.
SOLUTION
Let U : The set of all human beings.
S : The set of all share brokers.
C : The set of all chartered accountants.
The above Venn diagram represents the truth of the given statement i.e., S ∩ C ≠ φ.
Draw a Venn diagram for the truth of the following statement.
No wicket keeper is bowler, in a cricket team.
SOLUTION
Let U : The set of all human beings.
W : The set of all wicket keepers.
B : The set of all bowlers.
The above Venn diagram represents the truth of the given statement i.e., W ∩ B = φ.
Represent the following statement by the Venn diagram.
Some non-resident Indians are not rich.
SOLUTION
Let, U : The set of all human beings.
N : The set of all non-resident Indians.
R : The set of all rich people.
The above Venn diagram represents the truth of the given statement i.e., N - R ≠ φ
Represent the following statement by the Venn diagram.
No circle is rectangle.
SOLUTION
Let, U : The set of all geometrical figures.
C : The set of all circles.
R : The set of all rectangles.
The above Venn diagram represents the truth of the given statement i.e., C ∩ R = φ.
Represent the following statement by the Venn diagram.
If n is a prime number and n ≠ 2, then it is odd.
SOLUTION
Let, U : The set of all real numbers.
P : The set of all prime numbers n and n ≠ 2.
O : The set of all odd numbers.
The above Venn diagram represents the truth of the given statement i.e., P ⊂ O.
MISCELLANEOUS EXERCISE 1 [PAGES 29 - 34]
Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board Chapter 1 Mathematical Logic Miscellaneous Exercise 1 [Pages 29 - 34]
Choose the correct alternative :
Which of the following is not a statement?
Smoking is injuries to health
2 + 2 = 4
2 is the only even prime number.
Come here
SOLUTION
Come here
QUESTION
Choose the correct alternative :
Which of the following is an open statement?
x is a natural number.
Give answer a glass of water.
WIsh you best of luck.
Good morning to all.
SOLUTION
QUESTION
Choose the correct alternative :
Let p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r). Then, this law is known as.
commutative law
associative law
De-Morgan's law
distributive law
SOLUTION
QUESTION
Choose the correct alternative :
The false statement in the following is
p ∧ (∼ p) is contradiction
(p → q) ↔ (∼ q → ∼ p) is a contradiction.
~ (∼ p) ↔ p is a tautology
p ∨ (∼ p) ↔ p is a tautology
SOLUTION
QUESTION
Choose the correct alternative :
For the following three statements
p : 2 is an even number.
q : 2 is a prime number.
r : Sum of two prime numbers is always even.
Then, the symbolic statement (p ∧ q) → ∼ r means.
2 is an even and prime number and the sum of two prime numbers is always even.
2 is an even and prime number and the sum of two prime numbers is not always even.
If 2 is an even and prime number, then the sum of two prime numbers is not always even.
If 2 is an even and prime number, then the sum of two prime numbers is also even.
SOLUTION
QUESTION
Choose the correct alternative :
If p : He is intelligent.
q : He is strong
Then, symbolic form of statement “It is wrong that, he is intelligent or strong” is
∼p ∨ ∼ p
∼ (p ∧ q)
∼ (p ∨ q)
p ∨ ∼ q
SOLUTION
QUESTION
Choose the correct alternative :
The negation of the proposition “If 2 is prime, then 3 is odd”, is
If 2 is not prime, then 3 is not odd.
2 is prime and 3 is not odd.
2 is not prime and 3 is odd.
If 2 is not prime, then 3 is odd.
SOLUTION
QUESTION
Choose the correct alternative :
The statement (∼ p ∧ q) ∨∼ q is
p ∨ q
p ∧ q
∼ (p ∨ q)
∼ (p ∧ q)
SOLUTION
QUESTION
Choose the correct alternative :
Which of the following is always true?
(p → q) ≡ ∼ q → ∼ p
∼ (p ∨ q) ≡ ∼ p ∨ ∼ q
∼ (p → q) ≡ p ∧ ∼ q
∼ (p ∨ q) ≡ ∼ p ∧ ∼ q
SOLUTION
QUESTION
Choose the correct alternative :
∼ (p ∨ q) ∨ (∼ p ∧ q) is logically equivalent to
∼ p
p
q
∼ q
SOLUTION
QUESTION
Choose the correct alternative :
If p and q are two statements then (p → q) ↔ (∼ q → ∼ p) is
contradiction
tautology
Neither (i) not (ii)
None of the these
SOLUTION
QUESTION
Choose the correct alternative :
If p is the sentence ‘This statement is false’ then
truth value of p is T
truth value of p is F
p is both true and false
p is neither true nor false
SOLUTION
QUESTION
Choose the correct alternative :
Conditional p → q is equivalent to
p → ∼ q
∼ p ∨ q
∼ p → ∼ q
p ∨∼q
SOLUTION
QUESTION
Choose the correct alternative :
Negation of the statement “This is false or That is true” is
That is true or This is false
That is true and This is false
That is true and That is false
That is false and That is true
SOLUTION
QUESTION
Choose the correct alternative :
If p is any statement then (p ∨ ∼ p) is a
contingency
contradiction
tautology
None of them
SOLUTION
QUESTION
Fill in the blanks :
The statement q → p is called as the ––––––––– of the statement p → q.
SOLUTION
The statement q → p is called as the Converse of the statement p → q.
QUESTION
Fill in the blanks :
Conjunction of two statement p and q is symbolically written as –––––––––.
SOLUTION
Conjunction of two statement p and q is symbolically written as p ∧ q.
QUESTION
Fill in the blanks :
If p ∨ q is true then truth value of ∼ p ∨ ∼ q is –––––––––.
SOLUTION
If p ∨ q is true then truth value of ∼ p ∨ ∼ q is F.
QUESTION
Fill in the blanks :
Negation of “some men are animal” is –––––––––.
SOLUTION
Negation of “some men are animal” is No men are animals.
QUESTION
Fill in the blanks :
Truth value of if x = 2, then x2 = − 4 is –––––––––.
SOLUTION
Truth value of if x = 2, then x2 = − 4 is F.
QUESTION
Fill in the blanks :
Inverse of statement pattern p ↔ q is given by –––––––––.
SOLUTION
Inverse of statement pattern p ↔ q is given by ∼ p → ∼ q.
QUESTION
Fill in the blanks :
p ↔ q is false when p and q have ––––––––– truth values.
SOLUTION
p ↔ q is false when p and q have different truth values.
QUESTION
Fill in the blanks :
Let p : the problem is easy. r : It is not challenging then verbal form of ∼ p → r is –––––––––.
SOLUTION
Let p : the problem is easy. r : It is not challenging then verbal form of ∼ p → r is If the problem is not easy them it is not challenging.
QUESTION
Fill in the blanks :
Truth value of 2 + 3 = 5 if and only if − 3 > − 9 is –––––––––.
SOLUTION
Truth value of 2 + 3 = 5 if and only if − 3 > − 9 is T.
QUESTION
State whether the following statement is True or False :
Truth value of 2 + 3 < 6 is F.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
There are 24 months in year is a statement.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
p ∨ q has truth value F is both p and q has truth value F.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
The negation of 10 + 20 = 30 is, it is false that 10 + 20 ≠ 30.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
Dual of (p ∧ ∼ q) ∨ t is (p ∨ ∼ q) ∨ C.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
Dual of “John and Ayub went to the forest” is “John and Ayub went to the forest”.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
“His birthday is on 29th February” is not a statement.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
x2 = 25 is true statement.
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
Truth value of
True
False
SOLUTION
QUESTION
State whether the following statement is True or False :
p ∧ t = p.
True
False
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
Ice cream Sundaes are my favourite.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
x + 3 = 8 ; x is variable.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
Read a lot to improve your writing skill.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
z is a positive number.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
(a + b)2 = a2 + 2ab + b2 for all a, b ∈ R.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
(2 + 1)2 = 9.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
Why are you sad?
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
How beautiful the flower is!
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
The square of any odd number is even.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
All integers are natural numbers.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
If x is real number then x2 ≥ 0.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
Do not come inside the room.
Is a statement
Is not a statement
SOLUTION
QUESTION
Solve the following :
State which of the following sentences are statements in logic.
What a horrible sight it was!
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
The square of every real number is positive.
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
Every parallelogram is a rhombus.
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
a2 − b2 = (a + b) (a − b) for all a, b ∈ R.
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
Please carry out my instruction.
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
The Himalayas is the highest mountain range.
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
(x − 2) (x − 3) = x2 − 5x + 6 for all x∈R.
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
What are the causes of rural unemployment?
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
0! = 1
Is a statement
Is not a statement
SOLUTION
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
The quadratic equation ax2 + bx + c = 0 (a ≠ 0) always has two real roots.
Is a statement
Is not a statement
SOLUTION
The quadratic equation ax2 + bx + c = 0 (a ≠ 0) always has two real roots is a statement.
Hence, its truth value is F.
QUESTION
Which of the following sentence is a statement? In case of a statement, write down the truth value.
What is happy ending?
Is a statement
Is not a statement
SOLUTION
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The Sun has set and Moon has risen.
SOLUTION
Let p : The sun has set.
q : The moon has risen
The symbolic form is p ∧ q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Mona likes Mathematics and Physics.
SOLUTION
Let p : Mona likes Mathematics
q : Mona likes Physics
The symbolic form is p ∧ q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
3 is prime number if 3 is perfect square number.
SOLUTION
Let p : 3 is a prime number.
q : 3 is a perfect square number.
The symbolic form is p ↔ q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Kavita is brilliant and brave.
SOLUTION
Let p : Kavita is brilliant.
q : Kavita is brave.
The symbolic form is p ∧ q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If Kiran drives the car, then Sameer will walk.
SOLUTION
Let p : Kiran drives the car.
q : Sameer will walk.
The symbolic form is p → q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The necessary condition for existence of a tangent to the curve of the function is continuity.
SOLUTION
The given statement can also be expressed as ‘If the function is continuous, then the tangent to the curve exists’.
Let p : The function is continuous
q : The tangent to the curve exists.
∴ p → q is the symbolic form of the given statement.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
To be brave is necessary and sufficient condition to climb the Mount Everest.
SOLUTION
Let p : To be brave
q : climb the Mount Everest
∴ p ↔ q is the symbolic form of the given statement.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
x3 + y3 = (x + y)3 if xy = 0.
SOLUTION
Let p : x3 + y3 = (x + y)3
q : xy = 0
∴ p ↔ q is the symbolic form of the given statement.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
The drug is effective though it has side effects.
SOLUTION
The given statement can also be expressed as “The drug is effective and it has side effects”
Let p : The drug is effective.
q : It has side effects.
∴ p ∧ q is the symbolic form of the given statement.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If a real number is not rational, then it must be irrational.
SOLUTION
Let p : A real number is not rational.
q : A real number must be irrational.
The symbolic form is p → q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that Ram is tall and handsome.
SOLUTION
Let p : Ram is tall.
q : Ram is handsome.
The symbolic form is ∼(p ∧ q).
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
Even though it is not cloudy, it is still raining.
SOLUTION
Let p : it is cloudy.
q : It is still raining.
The symbolic form is ~ p ∧ q.
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
It is not true that intelligent persons are neither polite nor helpful.
SOLUTION
Let p : Intelligent persons are neither polite nor helpful
The symbolic form is ∼ p.
Alternate method:
Let p : Intelligent persons are polite.
q : Intelligent persons are helpful.
The symbolic form is ~(~ p ∧ ~ q).
QUESTION
Assuming the first statement p and second as q. Write the following statement in symbolic form.
If the question paper is not easy then we shall not pass.
SOLUTION
Let p : The question paper is not easy.
q : We shall not pass.
The symbolic form is p → q.
QUESTION
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
Proof is lengthy and it is not interesting.
SOLUTION
p ∧ ∼ q
QUESTION
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
If proof is lengthy then it is interesting.
SOLUTION
p → q
QUESTION
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is not true that the proof is lengthy but it is interesting.
SOLUTION
∼(p ∧ q)
QUESTION
If p : Proof is lengthy.
q : It is interesting.
Express the following statement in symbolic form.
It is interesting iff the proof is lengthy.
SOLUTION
q ↔ p
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∨ r
SOLUTION
Sachin wins the match or he is the member of Rajya Sabha or Sachin is happy.
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → r
SOLUTION
If Sachin wins the match then he is happy.
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ p ∨ q
SOLUTION
Sachin does not win the match or he is the member of Rajya Sabha.
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → (p ∧ r)
SOLUTION
If sachin wins the match, then he is the member of Rajyasabha or he is happy.
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
p → q
SOLUTION
If Sachin wins the match then he is a member of Rajyasabha.
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
(p ∧ q) ∧ ∼ r
SOLUTION
Sachin wins the match and he is the member of Rajyasabha but he is not happy.
QUESTION
Let p : Sachin wins the match.
q : Sachin is a member of Rajya Sabha.
r : Sachin is happy.
Write the verbal statement of the following.
∼ (p ∨ q) ∧ r
SOLUTION
It is false that Sachin wins the match or he is the member of Rajyasabha but he is happy.
QUESTION
Determine the truth value of the following statement.
4 + 5 = 7 or 9 − 2 = 5
SOLUTION
Let p : 4 + 5 = 7
q : 9 – 2 = 5
The truth values of p and q are F and F respectively. The given statement in symbolic form is p ∨ q.
∴ p ∨ q ≡ F ∨ F ≡ F
∴ Truth value of the given statement is F.
QUESTION
Determine the truth value of the following statement.
If 9 > 1 then x2 − 2x + 1 = 0 for x = 1
SOLUTION
Let p : 9 > 1
q : x2 – 2x + 1 = 0 for x = 1
The truth values of p and q are T and T respectively. The given statement in symbolic form is p → q.
∴ p → q ≡ T → T ≡ T
∴ Truth value of the given statement is T.
QUESTION
Determine the truth value of the following statement.
x + y = 0 is the equation of a straight line if and only if y2 = 4x is the equation of the parabola.
SOLUTION
Let p : x + y = 0 is the equation of a straight line.
q : y2 = 4x is the equation of the parabola.
The truth values of p and q are T and T respectively.
The given statement in symbolic form is p ↔ q.
∴ p ↔ q ≡ T ↔ T ≡ T
∴ Truth value of the given statement is T.
QUESTION
Determine the truth value of the following statement.
It is not true that 2 + 3 = 6 or 12 + 3 =5
SOLUTION
Let p : 2 + 3 = 6
q : 12 + 3 = 5
The truth values of p and q are F and F respectively.
The given statement in symbolic form is ~(p ∨ q).
∴ ~(p ∨ q) ≡ ~(F ∨ F) ≡ ~F ≡ T
∴ Truth value of the given statement is T.
QUESTION
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are not high or stocks are rising.
SOLUTION
Given that the truth values of both p and q are T.
The symbolic form of the given statement is ~ p ∨ q.
∴ ~ p ∨ q ≡ ~ T ∨ T ≡ F ∨ T
Hence, truth value is T.
QUESTION
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high and stocks are rising if and only if stock prices are high.
SOLUTION
The symbolic form of the given statement is
(p ∧ q) ↔ p.
∴ (p ∧ q) ↔ p ≡ (T ∧ T) ↔ T
≡ T ↔ T
≡ T
Hence, truth value is T.
QUESTION
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
If stock prices are high then stocks are not rising.
SOLUTION
The Symbolic form of the given statement is p → ~ q.
∴ p → ~ q ≡ T → ~ T ≡ T → F ≡ F
Hence, truth value is F.
QUESTION
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
It is false that stocks are rising and stock prices are high.
SOLUTION
The symbolic form of the given statement is ~(q ∧ p).
∴ ~(q ∧ p) ≡ ~(T ∧ T) ≡ ~T ≡ F
Hence, truth value is F.
QUESTION
Assuming the following statement.
p : Stock prices are high.
q : Stocks are rising.
to be true, find the truth value of the following.
Stock prices are high or stocks are not rising iff stocks are rising.
SOLUTION
The symbolic form of the given statement is (p ∨ ~q) ↔ q.
∴ (p ∨ ~q) ↔ q ≡ (T ∨ ~T) ↔ T
≡ (T ∨ F) ↔ T
≡ T ↔ T
≡ T
Hence, truth value is T.
QUESTION
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If price increases, then demand falls.
SOLUTION
Let p : Prince increases.
q : demand falls.
The given statement is p → q.
But p → q ≡ ~p ∨ q.
The given statement can be written as ‘Price does not increase or demand falls’.
QUESTION
Rewrite the following statement without using conditional –
(Hint : p → q ≡ ∼ p ∨ q)
If demand falls, then price does not increase.
SOLUTION
Let p : demand falls.
q : Price does not increase.
The given statement is p → q.
But p → q ≡ ~ p ∨ q.
∴ The given statement can be written as ‘Demand does not fall or price does not increase’.
QUESTION
If p, q, r are statements with truth values T, T, F respectively determine the truth values of the following.
(p ∧ q) → ∼ p.
SOLUTION
(p ∧ q) → ∼ p ≡ (T ∧ T) → ∼ T
≡ T → F
≡ F.
Hence, truth value is F.
QUESTION
If p, q, r are statements with truth values T, T, F respectively determine the truth values of the following.
p ↔ (q → ∼ p)
SOLUTION
p ↔ (q → ∼ p) ≡ T ↔ (T → ∼ T)
≡ T ↔ (T → F)
≡ T ↔ F
≡ F
Hence, truth value is F.
QUESTION
If p, q, r are statements with truth values T, T, F respectively determine the truth values of the following.
(p ∧ ∼ q) ∨ (∼ p ∧ q)
SOLUTION
(p ∧ ∼ q) ∨ (∼ p ∧ q) ≡ (T ∧ ∼ T) ∨ (∼ T ∧ T)
≡ (T ∧ F) ∨ (F ∧ T)
≡ F ∨ F
≡ F
Hence, truth value is F.
QUESTION
If p, q, r are statements with truth values T, T, F respectively determine the truth values of the following.
∼ (p ∧ q) → ∼ (q ∧ p)
SOLUTION
∼ (p ∧ q) → ∼ (q ∧ p) ≡ ∼ (T ∧ T) → ∼ (T ∧ T)
≡ ~ T → ~ T
≡ F → F
≡ T
Hence, truth value is T.
QUESTION
If p, q, r are statements with truth values T, T, F respectively determine the truth values of the following.
∼ [(p → q) ↔ (p ∧ ∼ q)]
SOLUTION
∼[(p → q) ↔ (p ∧ ∼q)] ≡ ∼ [(T → T) ↔ (T ∧ ∼ T)]
≡ ~[T ↔ (T ∧ F)]
≡ ~(T ↔ F)
≡ ~ F
≡ T
Hence, truth value is T.
QUESTION
Write the negation of the following.
If ∆ABC is not equilateral, then it is not equiangular.
SOLUTION
Let p : ∆ ABC is not equilateral.
q : ∆ ABC is not equiangular.
The given statement is p → q.
Its negation is ~(p → q) ≡ p ∧ ~ q
∴ The negation of given statement is '∆ ABC is not equilateral and it is equiangular'.
QUESTION
Write the negation of the following.
Ramesh is intelligent and he is hard working.
SOLUTION
Let p : Ramesh is intelligent.
q : Ramesh is hard working.
The given statement is p ∧ q.
Its negation is ~(p ∧ q) ≡ ~ p ∨ ~ q
∴ The negation of the given statement is ‘Ramesh is not intelligent or he is not hard-working.’
QUESTION
Write the negation of the following.
An angle is a right angle if and only if it is of measure 90°.
SOLUTION
Let p : An angle is a right angle.
q : An angle is of measure 90°.
The given statement is p ↔ q.
Its negation is ~(p ↔ q) ≡ (p ∧ ~ q) ∨ (q ∧ ~ p)
∴ The negation of the given statement is ‘An angle is a right angle and it is not of measure 90° or an angle is of measure 90° and it is not a right angle.’
QUESTION
Write the negation of the following.
Kanchanganga is in India and Everest is in Nepal.
SOLUTION
Let p : Kanchanganga is in India.
q : Everest is in Nepal.
The given statement is p ∧ q.
Its negation is ~(p ∧ q) ≡ ~ p ∨ ~ q.
The negation of a given statement is ‘Kanchanganga is not in India or Everest is not in Nepal’.
QUESTION
Write the negation of the following.
If x ∈ A ∩ B, then x ∈ A and x ∈ B.
SOLUTION
Let p : x ∈ A ∩ B
q : x ∈ A
r : x ∈ B
The given statement is p → (q ∧ r).
Its negation is ~[p → (q ∧ r)], and
~[p → (q ∧ r)] ≡ p ∧ ~ (q ∧ r) ≡ p ∧ ~ q ∨ ~ r
∴ The negation of given statement is x ∈ A ∩ B and x ∉ A or x ∉ B.
QUESTION
Construct the truth table for the following statement pattern.
(p ∧ ~q) ↔ (q → p)
SOLUTION
| p | q | ~q | p∧~q | q→p | (p∧~q)↔(q→p) |
| T | T | F | F | T | F |
| T | F | T | T | T | T |
| F | T | F | F | F | T |
| F | F | T | F | T | F |
QUESTION
Construct the truth table for the following statement pattern.
(~p ∨ q) ∧ (~p ∧ ~q)
SOLUTION
| p | q | ~p | ~q | ~p∨q | ~p∧~q | (~p∨q)∧(~p∧~q) |
| T | T | F | F | T | F | F |
| T | F | F | T | F | F | F |
| F | T | T | F | T | F | F |
| F | F | T | T | T | T | T |
QUESTION
Construct the truth table for the following statement pattern.
(p ∧ r) → (p ∨ ~q)
SOLUTION
| p | q | r | ~q | p∧r | p∨~q | (p∧r)→(p∨~q) |
| T | T | T | F | T | T | T |
| T | T | F | F | F | T | T |
| T | F | T | T | T | T | T |
| T | F | F | T | F | T | T |
| F | T | T | F | F | F | T |
| F | T | F | F | F | F | T |
| F | F | T | T | F | T | T |
| F | F | F | T | F | T | T |
QUESTION
Construct the truth table for the following statement pattern.
(p ∨ r) → ~(q ∧ r)
SOLUTION
| p | q | r | p∨r | q∧r | ~q∧r) | (p∨r)→~(q ∧ r) |
| T | T | T | T | T | F | F |
| T | T | F | T | F | T | T |
| T | F | T | T | F | T | T |
| T | F | F | T | F | T | T |
| F | T | T | T | T | F | F |
| F | T | F | F | F | T | T |
| F | F | T | T | F | T | T |
| F | F | F | F | F | T | T |
QUESTION
Construct the truth table for the following statement pattern.
(p ∨ ~q) → (r ∧ p)
SOLUTION
| p | q | r | ~q | p∨~q | r∧p | (p∨~q)→(r∧p) |
| T | T | T | F | T | T | T |
| T | T | F | F | T | F | F |
| T | F | T | T | T | T | T |
| T | F | F | T | T | F | F |
| F | T | T | F | F | F | T |
| F | T | F | F | F | F | T |
| F | F | T | T | T | F | F |
| F | F | F | T | T | F | F |
QUESTION
What is tautology? What is contradiction?
Show that the negation of a tautology is a contradiction and the negation of a contradiction is a tautology.
SOLUTION
- Tautology:
A statement pattern having truth value always T, irrespective of the truth values of its component statement is called a tautology. - Contradiction:
A statement pattern having truth value always F, irrespective of the truth values of its component statement is called a contradiction.
Let Statement p tautology. Consider, truth table
| p | ~ p |
| T | F |
i.e., negation of tautology is contradiction.
Let statement of contradiction. Consider, truth table
| q | ~ q |
| F | T |
i.e., negation of contradiction is tautology.
QUESTION
Determine whether the following statement pattern is a tautology, contradiction, or contingency.
[(p ∧ q) ∨ (~p)] ∨ [p ∧ (~ q)]
SOLUTION
| p | q | ~p | ~q | p∧q | (p∧q)∨(~p) | p∧~q | [(p∧q)∨(~p)]∨[p∧(~q)] |
| T | T | F | F | T | T | F | T |
| T | F | F | T | F | F | T | T |
| F | T | T | F | F | T | F | T |
| F | F | T | T | F | T | F | T |
All the truth values in the last column are T. Hence, it is a tautology.
QUESTION
Determine whether the following statement pattern is a tautology, contradiction, or contingency.
[(~p ∧ q) ∧ (q ∧ r)] ∨ (~q)
SOLUTION
| p | q | r | ~p | ~q | ~p∧q | q∧r | (~p∧q)∧(q∧r) | [(~p∧q)∧(q∧r)]∨(~q) |
| T | T | T | F | F | F | T | F | F |
| T | T | F | F | F | F | F | F | F |
| T | F | T | F | T | F | F | F | T |
| T | F | F | F | T | F | F | F | T |
| F | T | T | T | F | T | T | T | T |
| F | T | F | T | F | T | F | F | F |
| F | F | T | T | T | F | F | F | T |
| F | F | F | T | T | F | F | F | T |
Truth values in the last column are not identical. Hence, it is contingency.
QUESTION
Determine whether the following statement pattern is a tautology, contradiction, or contingency.
[~(p ∨ q) → p] ↔ [(~p) ∧ (~q)]
SOLUTION
| p | q | ~p | ~q | p∨q | ~(p∨q) | ~(p∨q)→p | (~p)∧(~q) | [~(p∨q)→p]↔[(~p)∧(~q)] |
| T | T | F | F | T | F | T | F | F |
| T | F | F | T | T | F | T | F | F |
| F | T | T | F | T | F | T | F | F |
| F | F | T | T | F | T | F | T | F |
All the truth values in the last column are F. Hence, it is a contradiction.
QUESTION
Determine whether the following statement pattern is a tautology, contradiction, or contingency.
[~(p ∧ q) → p] ↔ [(~p) ∧ (~q)]
SOLUTION
| p | q | ~p | ~q | p∧q | ~(p∧q) | ~(p∧q)→p | (~p)∧(~q) | [~(p∧q)→p]↔[(~p)∧(~q)] |
| T | T | F | F | T | F | T | F | F |
| T | F | F | T | F | T | T | F | F |
| F | T | T | F | F | T | F | F | T |
| F | F | T | T | F | T | F | T | F |
Truth values in the last column are not identical. Hence, it is contingency.
QUESTION
Determine whether the following statement pattern is a tautology, contradiction, or contingency.
[P → (~q ∨ r)] ↔ ~[p → (q → r)]
SOLUTION
| p | q | r | ~q | ~q∨r | q→r | p→(q→r) | P→(~q∨r) | ~[p→(q→r)] | [P→(~q∨r)]↔~[p → (q → r)] |
| T | T | T | F | T | T | T | T | F | F |
| T | T | F | F | F | F | F | F | T | F |
| T | F | T | T | T | T | T | T | F | F |
| T | F | F | T | T | T | T | T | F | F |
| F | T | T | F | T | T | T | T | F | F |
| F | T | F | F | F | F | T | T | F | F |
| F | F | T | T | T | T | T | T | F | F |
| F | F | F | T | T | T | T | T | F | F |
All the truth values in the last column are F. Hence, it is contradiction.
QUESTION
Using the truth table, prove the following logical equivalence.
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| p | q | r | q∨r | p∧(q∨r) | p∧q | p∧r | (p∧q)∨(p∧r) |
| T | T | T | T | T | T | T | T |
| T | T | F | T | T | T | F | T |
| T | F | T | T | T | F | T | T |
| T | F | F | F | F | F | F | F |
| F | T | T | T | F | F | F | F |
| F | T | F | T | F | F | F | F |
| F | F | T | T | F | F | F | F |
| F | F | F | F | F | F | F | F |
In the above truth table, the entries in columns 5 and 8 are identical.
∴ p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
QUESTION
Using the truth table, prove the following logical equivalence.
[~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| p | q | r | p∨q | ~(p∨q) | [~(p∨q)∨(p∨q)] | [~(p∨q)∨(p∨q)]∧r |
| T | T | T | T | F | T | T |
| T | T | F | T | F | T | F |
| T | F | T | T | F | T | T |
| T | F | F | T | F | T | F |
| F | T | T | T | F | T | T |
| F | T | F | T | F | T | F |
| F | F | T | F | T | T | T |
| F | F | F | F | T | T | F |
In the above truth table, the entries in columns 3 and 7 are identical.
∴ [~(p ∨ q) ∨ (p ∨ q)] ∧ r ≡ r
QUESTION
Using the truth table, prove the following logical equivalence.
p ∧ (~p ∨ q) ≡ p ∧ q
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | ~p | ~p∨q | p∧(~p∨q) | p∧q |
| T | T | F | T | T | T |
| T | F | F | F | F | F |
| F | T | T | T | F | F |
| F | F | T | T | F | F |
In the above truth table, the entries in columns 5 and 6 are identical.
∴ p ∧ (~p ∨ q) ≡ p ∧ q
QUESTION
Using the truth table, prove the following logical equivalence.
p ↔ q ≡ ~(p ∧ ~q) ∧ ~(q ∧ ~p)
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| p | q | ~p | ~q | p↔q | p∧~q | ~(p∧~q) | (q∧~p) | ~(q∧~p) | ~(p∧~q)∧~(q ∧ ~p) |
| T | T | F | F | T | F | T | F | T | T |
| T | F | F | T | F | T | F | F | T | F |
| F | T | T | F | F | F | T | T | F | F |
| F | F | T | T | T | F | T | F | T | T |
In the above truth table, the entries in columns 5 and 10 are identical.
∴ p ↔ q ≡ ~(p ∧ ~q) ∧ ~(q ∧ ~p)
QUESTION
Using the truth table, prove the following logical equivalence.
~p ∧ q ≡ [(p ∨ q)] ∧ ~p
SOLUTION
| 1 | 2 | 3 | 4 | 5 | 6 |
| p | q | ~p | ~p∧q | (p∨q) | (p∨q)∧~p |
| T | T | F | F | T | F |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | F | T | F | F | F |
In the above truth table, the entries in columns 4 and 6 are identical.
∴ ~p ∧ q ≡ [(p ∨ q)] ∧ ~p
QUESTION
Write the converse, inverse, contrapositive of the following statement.
If 2 + 5 = 10, then 4 + 10 = 20.
SOLUTION
Let p : 2 + 5 = 10
q : 4 + 10 = 20
∴ The given statement is p → q.
Its converse is q → p.
If 4 + 10 = 20, then 2 + 5 = 10
Its inverse is ~p → ~q.
If 2 + 5 ≠ 10 then 4 + 10 ≠ 20.
Its contrapositive is ~q → ~p.
If 4 + 10 ≠ 20 then 2 + 5 ≠ 10.
QUESTION
Write the converse, inverse, contrapositive of the following statement.
If a man is bachelor, then he is happy.
SOLUTION
Let p : A man is bachelor.
q : A man is happy.
∴ The given statement is p → q.
Its converse is q → p.
If a man is happy then he is bachelor.
Its inverse is ~p → ~q.
If a man is not bachelor then he is not happy.
Its contrapositive is ~q → ~p.
If a man is not happy then he is not bachelor.
QUESTION
Write the converse, inverse, contrapositive of the following statement.
If I do not work hard, then I do not prosper.
SOLUTION
Let p : I do not work hard.
q : I do not prosper.
∴ The given statement is p → q.
Its converse is q → p.
If I do not prosper then I do not work hard.
Its inverse is ~p → ~q.
If I work hard then I prosper.
Its contrapositive is ~q → ~p.
If I prosper then I work hard.
QUESTION
State the dual of the following statement by applying the principle of duality.
(p ∧ ~q) ∨ (~ p ∧ q) ≡ (p ∨ q) ∧ ~(p ∧ q)
SOLUTION
(p ∨ ~q) ∧ (~ p ∨ q) ≡ (p ∧ q) ∨ ~(p ∨ q)
QUESTION
State the dual of the following statement by applying the principle of duality.
p ∨ (q ∨ r) ≡ ~[(p ∧ q) ∨ (r ∨ s)]
SOLUTION
p ∧ (q ∧ r) ≡ ~[(p ∨ q) ∧ (r ∧ s)]
QUESTION
State the dual of the following statement by applying the principle of duality.
2 is even number or 9 is a perfect square.
SOLUTION
2 is even number and 9 is a perfect square.
QUESTION
Rewrite the following statement without using the connective ‘If ... then’.
If a quadrilateral is rhombus then it is not a square.
SOLUTION
Let p : A quadrilateral is rhombus.
q : A quadrilateral is not a square.
The given statement is p → q.
But p → q ≡ ~p ∨ q.
∴ The given statement can be written as ‘A quadrilateral is not a rhombus or it is not a square’.
QUESTION
Rewrite the following statement without using the connective ‘If ... then’.
If 10 − 3 = 7 then 10 × 3 ≠ 30.
SOLUTION
Let p : 10 − 3 = 7
q : 10 × 3 ≠ 30
The given statement is p → q.
But p → q ≡ ~p ∨ q.
∴ The given statement can be written as
'10 - 3 ≠ 7 or 10 × 3 ≠ 30'.
QUESTION
Rewrite the following statement without using the connective ‘If ... then’.
If it rains then the principal declares a holiday.
SOLUTION
Let p : It rains.
q : The principal declares a holiday.
The given statement is p → q.
But p → q ≡ ~p ∨ q.
∴ The given statement can be written as ‘It does not rain or the principal declares a holiday’.
QUESTION
Write the dual of the following.
(~p ∧ q) ∨ (p ∧ ~q) ∨ (~p ∧ ~q)
SOLUTION
(~p ∨ q) ∧ (p ∨ ~q) ∧ (~p ∨ ~q)
QUESTION
Write the dual of the following.
(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
SOLUTION
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)
QUESTION
Write the dual of the following.
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (q ∨ r)
SOLUTION
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (q ∧ r)
QUESTION
Write the dual of the following.
~(p ∨ q) ≡ ~p ∧ ~q
SOLUTION
~(p ∧ q) ≡ ~p ∨ ~q
QUESTION
Consider the following statements.
i. If D is dog, then D is very good.
ii. If D is very good, then D is dog.
iii. If D is not very good, then D is not a dog.
iv. If D is not a dog, then D is not very good. Identify the pairs of statements having the same meaning. Justify.
SOLUTION
Let p : D is dog.
q : D is very good.
Then the given statement in the symbolic form is i. p → q
ii. q → p
iii. ~q → ~p
iv. ~p → ~q
Since a statement and its contrapositive are equivalent, statements (i) and (iii) have the same meaning.
Since converse and inverse of a compound statement are equivalent, statements (ii) and (iv) have same meaning.
QUESTION
Express the truth of the following statement by the Venn diagram.
All men are mortal.
SOLUTION
U : The set of all human being
A : The set of all men
B : The set of all mortal
The above Venn diagram represents the truth of the given statement, i.e. A ⊂ B.
QUESTION
Express the truth of the following statement by the Venn diagram.
Some persons are not politician.
SOLUTION
U : The set of all human beings.
X : The set of all persons.
Y : The set of all politician
The above Venn diagram represents the truth of the given statement, i.e. Y - X ≠ Φ
QUESTION
Express the truth of the following statement by the Venn diagram.
Some members of the present Indian cricket are not committed.
SOLUTION
U : The set of all human beings.
M : The set of all members of the present Indian cricket.
C : The set of all committed members of the present Indian cricket.
The above Venn diagram represents the truth of the given statement, i.e. C - M = Φ
QUESTION
Express the truth of the following statement by the Venn diagram.
No child is an adult.
SOLUTION
U : Set of all human beings.
C : Set of all child.
A : Set of all Adult.
The above Venn diagram represents the truth of the given statement, i.e. C ∩ A = Φ
QUESTION
If A = {2, 3, 4, 5, 6, 7, 8}, determine the truth value of the following statement.
∃ x ∈ A, such that 3x + 2 > 9
SOLUTION
For x = 3, 3x + 2 = 3(3) + 2 = 9 + 2 = 11 > 9
∴ x = 3 satisfies the equation 3x + 2 > 9.
∴ The given statement is true.
∴ Its truth value is T.
QUESTION
If A = {2, 3, 4, 5, 6, 7, 8}, determine the truth value of the following statement.
∀ x ∈ A, x2 < 18.
SOLUTION
For x = 5, x2 = 52 = 25 < 18
∴ x = 5 does not satisfies the equation x2 < 18.
∴ The given statement is false.
∴ Its truth value is F.
QUESTION
If A = {2, 3, 4, 5, 6, 7, 8}, determine the truth value of the following statement.
∃ x ∈ A, such that x + 3 < 11.
SOLUTION
For x = 2, x + 3 = 2 + 3 = 5 < 11.
∴ x = 2 satisfies the equation x + 3 < 11.
∴ The given statement is true.
∴ Its truth value is T.
QUESTION
If A = {2, 3, 4, 5, 6, 7, 8}, determine the truth value of the following statement.
∀ x ∈ A, x2 + 2 ≥ 5.
SOLUTION
There is no x in A which satisfies x2 + 2 ≥ 5.
∴ The given statement is false.
∴ Its truth value is F.
QUESTION
Write the negation of the following statement.
7 is prime number and Tajmahal is in Agra.
SOLUTION
Let p : 7 is prime number.
q : Tajmahal is in Agra.
The given statement in symbolic form is p ∧ q.
Its negation is ~(p ∧ q) ≡ ~p ∨ ~q.
∴ The negation of given statement is '7 is not prime number or Tajmahal is not in Agra.'
QUESTION
Write the negation of the following statement.
10 > 5 and 3 < 8
SOLUTION
Let p : 10 > 5.
q : 3 < 8.
The given statement in symbolic form is p ∧ q.
Its negation is ~(p ∧ q) ≡ ~p ∨ ~q.
∴ The negation of given statement is '10 ≤ 5 or 3 ≥ 8.'
QUESTION
Write the negation of the following statement.
I will have tea or coffee.
SOLUTION
Let p : I will have tea.
q : I will have coffee.
The given statement in symbolic form is p ∨ q.
Its negation is ~(p ∨ q) ≡ ~p ∧ ~q.
∴ The negation of given statement is ‘I will not have tea and coffee’.
QUESTION
Write the negation of the following statement.
∀ n ∈ N, n + 3 > 9.
SOLUTION
∃ n ∈ N such that n + 3 ≤ 9.
QUESTION
Write the negation of the following statement.
∃ n ∈ A, such that x + 5 < 11.
SOLUTION
∀ x ∈ A, x + 5 ≤ 11
